
以前に勉強したDeep Q-Network(DQN)を、やっぱり離散的な状態を返す簡単なゲームでなく、連続的な状態のゲームにも適用してみたいと思い、久しぶりにまた勉強しました。
最近の深層強化学習の研究を見てみたところ、DQNからさらに進化していて、A3Cなるものまで登場していましたので、少しばかりそちらについても触れてみます。
環境(CartPole-v0)について
前回は迷路探索の問題でしたので、状態が「プレイヤーはどこにいるのか」といった離散的な値で表すことができました。
今回扱う環境は CartPole というゲームになります。
Open AI Gymによる説明とゲームの様子が下記になります。
CartPole-v0
A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track. The system is controlled by applying a force of +1 or -1 to the cart. The pendulum starts upright, and the goal is to prevent it from falling over. A reward of +1 is provided for every timestep that the pole remains upright. The episode ends when the pole is more than 15 degrees from vertical, or the cart moves more than 2.4 units from the center.
つまり、台車の上に棒(ポール)を立て、その棒が倒れてしまわないように、台車を右左に動かして、バランスよく立て続けるといったゲームです。
小学生の男子が箒を手のひらに乗せてバランスを保ち続けるといった遊びをやることがあると思いますが、あれと一緒です。(自分の小学校の時はよくありました笑)
強化学習では古典的によく使われてきた環境のようで、Open AI Gymにも環境が用意されています。
ゲームのルールについてまとめると下記のようになります。
- 状態は、棒の(横軸座標、横軸速度、ポール角度、ポール角速度)が連続値として観測できる
- 行動は、台車を左で動かすか、右へ動かすかの2値
- 棒が一定角度傾いてしまったらゲーム終了
- 台車が中心から一定距離を離れてしまってもゲーム終了
- 報酬は棒が立っている限り得られ続ける
- 棒が一定角度傾いてしまったら報酬なし(ただし、台車の位置に関しては問われないので、一定距離離れてしまっても報酬としては得られている状態になる)
実際にOpen AI Gymから環境を読み込んで、ランダムに行動を取り続けてみたときの各値が下記のようになります。
import gym
# 環境の確認
env = gym.make("CartPole-v0")
print("observation space num: ", env.observation_space.shape[0])
print("action space num: ", env.action_space.n)
pobs = env.reset()
done = False
while not done:
act = env.action_space.sample()
obs, reward, done, _ = env.step(act)
print(pobs, act, reward, obs, done)
pobs = obs
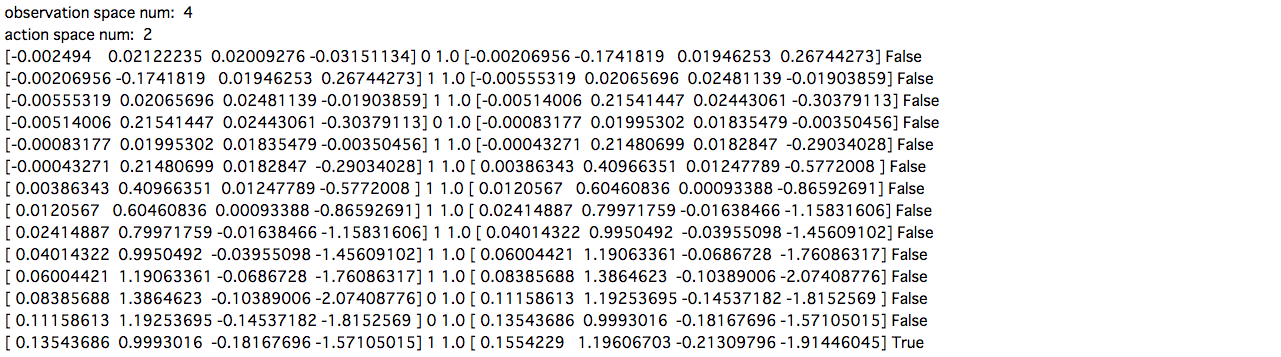
これらの値を使って深層強化学習を実装し、棒を長く立て続けられるように台車の動きを学習させてみます。
Deep Q-Network (DQN)
前回にも説明しましたが、復習します。
状態空間(環境がとりうる状態の集合)を ![]() 、行動空間(エージェントがとりうる行動の集合)を
、行動空間(エージェントがとりうる行動の集合)を ![]() 、政策(ポリシー)を
、政策(ポリシー)を ![]() 、報酬関数を
、報酬関数を ![]() とします。
とします。
エージェントは時刻 ![]() の状態
の状態 ![]() において、政策
において、政策 ![]() にしたがって行動
にしたがって行動 ![]() を選択し、次の状態
を選択し、次の状態 ![]() に遷移して、報酬
に遷移して、報酬 ![]() を得ます。
を得ます。
この時において、累積報酬 ![]() を最大化することが強化学習の目的でした。
を最大化することが強化学習の目的でした。
これは、期待累積報酬を最大化する最適政策 ![]() を求めることで、目的が達成できます。
を求めることで、目的が達成できます。
そこで、 ![]() にしたがった時の期待累積報酬を表す行動価値関数
にしたがった時の期待累積報酬を表す行動価値関数 ![]() を考え、これの最適関数
を考え、これの最適関数 ![]() を求めることで、
を求めることで、 ![]() として最適政策を求めることができます。
として最適政策を求めることができます。
強化学習の代表的な手法である Q-learningでは、行動価値関数 ![]() で価値の高い行動を選択し、状態・報酬の観測を繰り返すことで、次の状態での
で価値の高い行動を選択し、状態・報酬の観測を繰り返すことで、次の状態での ![]() の値と現時点での
の値と現時点での ![]() の値の間に生じるTD誤差を使って、最適な行動価値関数を推定します。
の値の間に生じるTD誤差を使って、最適な行動価値関数を推定します。
![]()
しかし、この場合、状態数や行動数がとても大きい数であったり、あるいは連続的であるなどの場合には、組み合わせの数が非常に多くなってしまい、計算させるのが困難なものになってしまいます。
そこで、Deep Q-Network(DQN)では、こういった場合において、![]() をテーブルではなく、関数(深層学習)で近似するということを考えます。
をテーブルではなく、関数(深層学習)で近似するということを考えます。
ただし、ここで近似する深層学習のネットワークは、状態×行動を入力とするのではなく、状態を入力して行動の ![]() 値を出力するネットワークを構成します。
値を出力するネットワークを構成します。
Q-learningと同様に、![]() を
を ![]() に近づけたいと考えるので、後者を教師信号
に近づけたいと考えるので、後者を教師信号 ![]() として、現在の
として、現在の ![]() との誤差関数
との誤差関数 ![]() を使ってネットワークを学習させます。
を使ってネットワークを学習させます。
![]()
![]()
またDQNでは、以上の学習アルゴリズムに加えて、下記のような工夫を加えることで、ネットワークを学習させることができました。
Experience replay
- エージェントが繰り返し行動して得られた経験は時系列に獲得するが、経験に相関があるとネットワークが過学習してしまう
- そこで、保存した経験からランダムに選んで学習させる
Freezing the target network
- TD誤差の目標値に古い
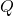 (target
(target 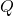 -network)を使う
-network)を使う 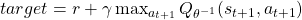
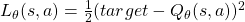
- 一定周期で学習中の
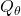 のパラメータと同期(
のパラメータと同期(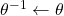 )
)
Clipping rewards
- 報酬のスケールを、正スコア+1、負スコア−1といったように統一する
Skipping frames
- 毎フレームで行動選択を行うと計算コストがかかる上、毎フレームで行動をする必要はない
- よって、数フレームおきに行動選択を行うようにする
以上、復習が長くなってしまいましたが、これをOpen AI GymのCartPoleに対して実装してみました。
今回はニューラルネットワークのライブラリはPyTorchを利用しました。
GitHub: https://github.com/Gin04gh/open_ai_gym/blob/master/DQN_PyTorch_CartPole.ipynb
移設しました。
GitHub: https://github.com/Gin04gh/datascience/blob/master/open_ai/dqn_pytorch_cartpole.ipynb
import copy
import time
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import gym
from gym import wrappers
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
# 環境
MONITOR = False
env = gym.make("CartPole-v0")
if MONITOR:
env = wrappers.Monitor(env, "./tmp", force=True)
obs_num = env.observation_space.shape[0]
acts_num = env.action_space.n
HIDDEN_SIZE = 100
class NN(nn.Module):
def __init__(self):
super(NN, self).__init__()
self.fc1 = nn.Linear(obs_num, HIDDEN_SIZE)
self.fc2 = nn.Linear(HIDDEN_SIZE, HIDDEN_SIZE)
self.fc3 = nn.Linear(HIDDEN_SIZE, HIDDEN_SIZE)
self.fc4 = nn.Linear(HIDDEN_SIZE, acts_num)
def __call__(self, x):
h = F.relu(self.fc1(x))
h = F.relu(self.fc2(h))
h = F.relu(self.fc3(h))
y = F.relu(self.fc4(h))
return y
# 定数
EPOCH_NUM = 3000 # エポック数
STEP_MAX = 200 # 最高ステップ数
MEMORY_SIZE = 200 # メモリサイズいくつで学習を開始するか
BATCH_SIZE = 50 # バッチサイズ
EPSILON = 1.0 # ε-greedy法
EPSILON_DECREASE = 0.001 # εの減少値
EPSILON_MIN = 0.1 # εの下限
START_REDUCE_EPSILON = 200 # εを減少させるステップ数
TRAIN_FREQ = 10 # Q関数の学習間隔
UPDATE_TARGET_Q_FREQ = 20 # Q関数の更新間隔
GAMMA = 0.97 # 割引率
LOG_FREQ = 1000 # ログ出力の間隔
# モデル
Q = NN() # 近似Q関数
Q_ast = copy.deepcopy(Q)
optimizer = optim.RMSprop(Q.parameters(), lr=0.00015, alpha=0.95, eps=0.01)
total_step = 0 # 総ステップ(行動)数
memory = [] # メモリ
total_rewards = [] # 累積報酬記録用リスト
# 学習開始
print("Train")
print("\t".join(["epoch", "EPSILON", "reward", "total_step", "elapsed_time"]))
start = time.time()
for epoch in range(EPOCH_NUM):
pobs = env.reset() # 環境初期化
step = 0 # ステップ数
done = False # ゲーム終了フラグ
total_reward = 0 # 累積報酬
while not done and step < STEP_MAX:
if MONITOR:
env.render()
# 行動選択
pact = env.action_space.sample()
# ε-greedy法
if np.random.rand() > EPSILON:
# 最適な行動を予測
pobs_ = np.array(pobs, dtype="float32").reshape((1, obs_num))
pobs_ = Variable(torch.from_numpy(pobs_))
pact = Q(pobs_)
maxs, indices = torch.max(pact.data, 1)
pact = indices.numpy()[0]
# 行動
obs, reward, done, _ = env.step(pact)
if done:
reward = -1
# メモリに蓄積
memory.append((pobs, pact, reward, obs, done)) # 状態、行動、報酬、行動後の状態、ゲーム終了フラグ
if len(memory) > MEMORY_SIZE: # メモリサイズを超えていれば消していく
memory.pop(0)
# 学習
if len(memory) == MEMORY_SIZE: # メモリサイズ分溜まっていれば学習
# 経験リプレイ
if total_step % TRAIN_FREQ == 0:
memory_ = np.random.permutation(memory)
memory_idx = range(len(memory_))
for i in memory_idx[::BATCH_SIZE]:
batch = np.array(memory_[i:i+BATCH_SIZE]) # 経験ミニバッチ
pobss = np.array(batch[:,0].tolist(), dtype="float32").reshape((BATCH_SIZE, obs_num))
pacts = np.array(batch[:,1].tolist(), dtype="int32")
rewards = np.array(batch[:,2].tolist(), dtype="int32")
obss = np.array(batch[:,3].tolist(), dtype="float32").reshape((BATCH_SIZE, obs_num))
dones = np.array(batch[:,4].tolist(), dtype="bool")
# set y
pobss_ = Variable(torch.from_numpy(pobss))
q = Q(pobss_)
obss_ = Variable(torch.from_numpy(obss))
maxs, indices = torch.max(Q_ast(obss_).data, 1)
maxq = maxs.numpy() # maxQ
target = copy.deepcopy(q.data.numpy())
for j in range(BATCH_SIZE):
target[j, pacts[j]] = rewards[j]+GAMMA*maxq[j]*(not dones[j]) # 教師信号
# Perform a gradient descent step
optimizer.zero_grad()
loss = nn.MSELoss()(q, Variable(torch.from_numpy(target)))
loss.backward()
optimizer.step()
# Q関数の更新
if total_step % UPDATE_TARGET_Q_FREQ == 0:
Q_ast = copy.deepcopy(Q)
# εの減少
if EPSILON > EPSILON_MIN and total_step > START_REDUCE_EPSILON:
EPSILON -= EPSILON_DECREASE
# 次の行動へ
total_reward += reward
step += 1
total_step += 1
pobs = obs
total_rewards.append(total_reward) # 累積報酬を記録
if (epoch+1) % LOG_FREQ == 0:
r = sum(total_rewards[((epoch+1)-LOG_FREQ):(epoch+1)])/LOG_FREQ # ログ出力間隔での平均累積報酬
elapsed_time = time.time()-start
print("\t".join(map(str,[epoch+1, EPSILON, r, total_step, str(elapsed_time)+"[sec]"]))) # ログ出力
start = time.time()
if MONITOR:
env.render(close=True)
plt.figure(figsize=(15,7))
resize = (len(total_rewards)//10, 10)
tmp = np.array(total_rewards, dtype="float32").reshape(resize)
tmp = np.average(tmp, axis=1)
plt.plot(tmp, color="cyan")
plt.show()
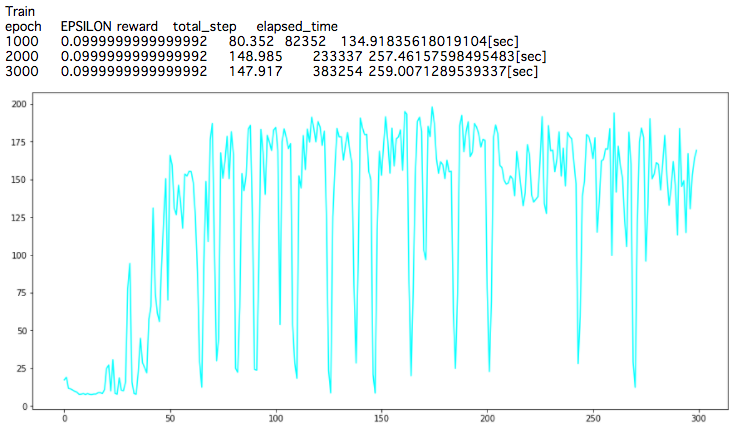
得られる累積報酬がエポックを重ねるごとに増えていっていることが確認できます。
200ステップまでしか行動しませんので、最高累積報酬は200です。
実際に動画で保存してみたものが以下になります。
最初の方のプレイ動画では、まだ学習が進んでいなく、すぐに棒が傾いてしまってゲームが終了する状態です。
学習が進んでいない状態
次に、学習が進んだ状態のプレイ動画が下記になります。(実は冒頭の環境説明の動画と同じものです)
まだ台車が少しずつ中心から移動してしまうようですが、バランスをとって棒を立て続けられるようになっています。
学習が進んだ状態
ひとまずはこのようにして学習できることが確認できました。
今回は、前回に一度DQNを実装しているため、ネットワークの実装などはスムーズに行えましたが、その一方で、ハイパーパラメータの調整に苦労しました。
DQNに関しては、勾配法のアルゴリズムの選択も含め、論文などで良いハイパーパラメータ値についての研究がされています。
最初はなかなかうまく学習しなかったのですが、アルゴリズムやハイパーパラメータをそのような研究を参考に設定し直すことで、うまく学習するようになりました。
DQNの改善研究やA3Cについて
上記のDQNが登場したのが2013年頃のことで、その後、こういった深層強化学習の分野の研究も盛んに行われるようになってから、様々なDQNの改良が登場しています。
最近DQNについて勉強した時にその辺りの研究についても調べる機会がありましたので、その中のいくつかについて簡単に触れてみようと思います。
Double DQN
論文は下記になります。
Deep reinforcement learning with double q-learning: https://arxiv.org/pdf/1509.06461.pdf
DQNでは、TD誤差計算時に目標値に大きすぎる値が設定されると、前の状態を過大評価してしまうという問題がありました。
そこで、2つの ![]() 関数を混ぜて学習をさせることで、TD誤差の計算の安定化を図ったものがDouble DQNです。
関数を混ぜて学習をさせることで、TD誤差の計算の安定化を図ったものがDouble DQNです。
具体的には、DQNにおける教師信号出力用のネットワークを ![]() 、そのコピーを
、そのコピーを ![]() とすると、
とすると、![]() でとるべき行動を
でとるべき行動を ![]() で決定し、その評価値を
で決定し、その評価値を ![]() で出力して
で出力して ![]() を更新します。
を更新します。
アルゴリズムを見れば分かるのですが、これはDQNのコードをほんの数行変更するだけで実現できます。
実装が下記になります。
GitHub: https://github.com/Gin04gh/open_ai_gym/blob/master/DoubleDQN_PyTorch_CartPole.ipynb
移設しました。
GitHub: https://github.com/Gin04gh/datascience/blob/master/open_ai/ddqn_pytorch_cartpole.ipynb
import copy
import time
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import gym
from gym import wrappers
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
# 環境
MONITOR = False
env = gym.make("CartPole-v0")
if MONITOR:
env = wrappers.Monitor(env, "./tmp", force=True)
obs_num = env.observation_space.shape[0]
acts_num = env.action_space.n
HIDDEN_SIZE = 100
class NN(nn.Module):
def __init__(self):
super(NN, self).__init__()
self.fc1 = nn.Linear(obs_num, HIDDEN_SIZE)
self.fc2 = nn.Linear(HIDDEN_SIZE, HIDDEN_SIZE)
self.fc3 = nn.Linear(HIDDEN_SIZE, HIDDEN_SIZE)
self.fc4 = nn.Linear(HIDDEN_SIZE, acts_num)
def __call__(self, x):
h = F.relu(self.fc1(x))
h = F.relu(self.fc2(h))
h = F.relu(self.fc3(h))
y = F.relu(self.fc4(h))
return y
# 定数
EPOCH_NUM = 3000 # エポック数
STEP_MAX = 200 # 最高ステップ数
MEMORY_SIZE = 200 # メモリサイズいくつで学習を開始するか
BATCH_SIZE = 50 # バッチサイズ
EPSILON = 1.0 # ε-greedy法
EPSILON_DECREASE = 0.001 # εの減少値
EPSILON_MIN = 0.1 # εの下限
START_REDUCE_EPSILON = 200 # εを減少させるステップ数
TRAIN_FREQ = 10 # Q関数の学習間隔
UPDATE_TARGET_Q_FREQ = 20 # Q関数の更新間隔
GAMMA = 0.97 # 割引率
LOG_FREQ = 1000 # ログ出力の間隔
# モデル
Q = NN() # 近似Q関数
Q_ast = copy.deepcopy(Q)
optimizer = optim.RMSprop(Q.parameters(), lr=0.00015, alpha=0.95, eps=0.01)
total_step = 0 # 総ステップ(行動)数
memory = [] # メモリ
total_rewards = [] # 累積報酬記録用リスト
# 学習開始
print("Train")
print("\t".join(["epoch", "EPSILON", "reward", "total_step", "elapsed_time"]))
start = time.time()
for epoch in range(EPOCH_NUM):
pobs = env.reset() # 環境初期化
step = 0 # ステップ数
done = False # ゲーム終了フラグ
total_reward = 0 # 累積報酬
while not done and step < STEP_MAX:
if MONITOR:
env.render()
# 行動選択
pact = env.action_space.sample()
# ε-greedy法
if np.random.rand() > EPSILON:
# 最適な行動を予測
pobs_ = np.array(pobs, dtype="float32").reshape((1, obs_num))
pobs_ = Variable(torch.from_numpy(pobs_))
pact = Q(pobs_)
maxs, indices = torch.max(pact.data, 1)
pact = indices.numpy()[0]
# 行動
obs, reward, done, _ = env.step(pact)
if done:
reward = -1
# メモリに蓄積
memory.append((pobs, pact, reward, obs, done)) # 状態、行動、報酬、行動後の状態、ゲーム終了フラグ
if len(memory) > MEMORY_SIZE: # メモリサイズを超えていれば消していく
memory.pop(0)
# 学習
if len(memory) == MEMORY_SIZE: # メモリサイズ分溜まっていれば学習
# 経験リプレイ
if total_step % TRAIN_FREQ == 0:
memory_ = np.random.permutation(memory)
memory_idx = range(len(memory_))
for i in memory_idx[::BATCH_SIZE]:
batch = np.array(memory_[i:i+BATCH_SIZE]) # 経験ミニバッチ
pobss = np.array(batch[:,0].tolist(), dtype="float32").reshape((BATCH_SIZE, obs_num))
pacts = np.array(batch[:,1].tolist(), dtype="int32")
rewards = np.array(batch[:,2].tolist(), dtype="int32")
obss = np.array(batch[:,3].tolist(), dtype="float32").reshape((BATCH_SIZE, obs_num))
dones = np.array(batch[:,4].tolist(), dtype="bool")
# set y_doubleq
pobss_ = Variable(torch.from_numpy(pobss))
q = Q(pobss_)
maxs, indices = torch.max(q.data, 1)
indices = indices.numpy()
obss_ = Variable(torch.from_numpy(obss))
maxqs = Q_ast(obss_).data.numpy() # ここからindiciesの行動の評価値で更新する
target = copy.deepcopy(q.data.numpy())
for j in range(BATCH_SIZE):
target[j, pacts[j]] = rewards[j]+GAMMA*maxqs[j, indices[j]]*(not dones[j]) # 教師信号
# Perform a gradient descent step
optimizer.zero_grad()
loss = nn.MSELoss()(q, Variable(torch.from_numpy(target)))
loss.backward()
optimizer.step()
# Q関数の更新
if total_step % UPDATE_TARGET_Q_FREQ == 0:
Q_ast = copy.deepcopy(Q)
# εの減少
if EPSILON > EPSILON_MIN and total_step > START_REDUCE_EPSILON:
EPSILON -= EPSILON_DECREASE
# 次の行動へ
total_reward += reward
step += 1
total_step += 1
pobs = obs
total_rewards.append(total_reward) # 累積報酬を記録
if (epoch+1) % LOG_FREQ == 0:
r = sum(total_rewards[((epoch+1)-LOG_FREQ):(epoch+1)])/LOG_FREQ # ログ出力間隔での平均累積報酬
elapsed_time = time.time()-start
print("\t".join(map(str,[epoch+1, EPSILON, r, total_step, str(elapsed_time)+"[sec]"]))) # ログ出力
start = time.time()
if MONITOR:
env.render(close=True)
plt.figure(figsize=(15,7))
resize = (len(total_rewards)//10, 10)
tmp = np.array(total_rewards, dtype="float32").reshape(resize)
tmp = np.average(tmp, axis=1)
plt.plot(tmp, color="cyan")
plt.show()
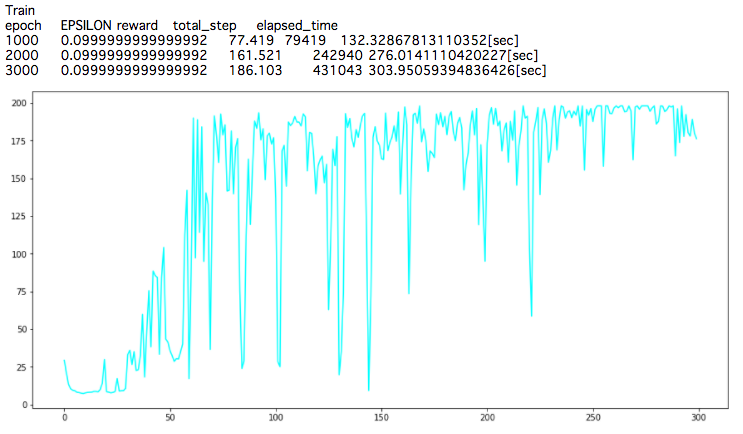
こちらも問題なく学習していくことが確認できます。
Dueling Double DQN
論文は下記になります。
Dueling Network Architectures for Deep Reinforcement Learning: https://arxiv.org/abs/1511.06581
もともとがDQNだっただけに、ネーミングがだんだんとネタのようになってきています笑
ここまでの方法では、 ![]() 関数において、1回の更新で1つの行動に対する価値しか更新ができません。
関数において、1回の更新で1つの行動に対する価値しか更新ができません。
そこでこの研究では、![]() 関数を状態価値関数
関数を状態価値関数 ![]() とAdvantage(行動優位)関数
とAdvantage(行動優位)関数 ![]() に分解して学習させます。
に分解して学習させます。
![]()
こうすることで、![]() については毎回更新ができるので、TD誤差の計算の伝播が早くなるようです。
については毎回更新ができるので、TD誤差の計算の伝播が早くなるようです。
単純に線形和で分解してしまうと、状態価値関数、Advantage関数がともに誤差を含めて学習してしまう恐れがあるため、これを防ぐために ![]() を加えるということをするようです。
を加えるということをするようです。
Prioritized Experience Replay
論文は下記になります。
Prioritized Experience Replay: https://arxiv.org/abs/1511.05952
名前の通りです。
DQNでは、経験からランダムに選んで学習してきているので、より学習に役立つ経験を優先して学習させるようにします。
具体的には、経験サンプルの重要性 ![]() を、TD誤差の絶対値
を、TD誤差の絶対値 ![]() (パラメータの更新幅とみなせる)を用いて表し、確率とした上で、経験サンプリングをします。
(パラメータの更新幅とみなせる)を用いて表し、確率とした上で、経験サンプリングをします。
![]()
こうすることで、TD誤差の大きい経験を優先して学習させられるようになります。
Gorila DQN
論文は下記になります。
Massively Parallel Methods for Deep Reinforcement Learning: https://arxiv.org/abs/1507.04296
「GOogle ReInforcement Learning Architecture」を略して「Gorila」で、頭の悪そうな名前になってしまいました。
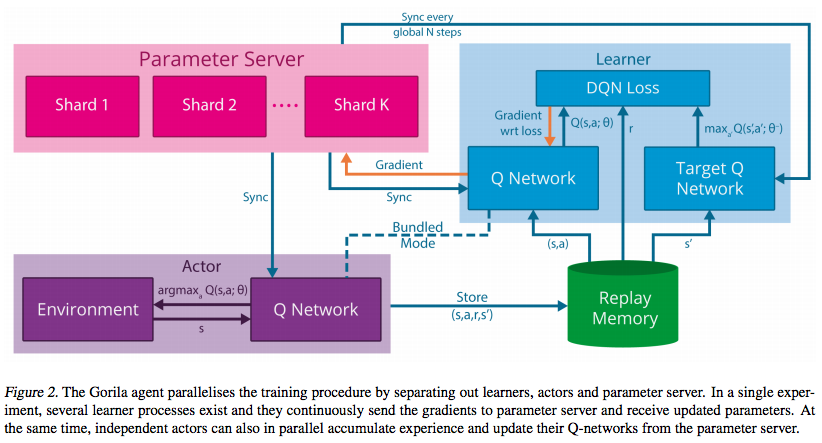
こちらは、これまでの学習アルゴリズムの改善とは少し違い、学習を並列分散させるということをします。
Memory(経験)を集めるActorと、誤差計算を行うLearnerに分けて、並列処理をすることで、DQNよりも高速に学習できたことが報告されています。
A3C
論文は下記になります。
Asynchronous Methods for Deep Reinforcement Learning: https://arxiv.org/pdf/1602.01783.pdf
Google DeepMind社により、2016年に発表された論文です。
Asynchronous Advantage Actor-Critic(A3C)は、これまでのDQNの学習アルゴリズムとは大きく変わってきます。
こちらも並列処理をさせることで、GPUを使ったDQNよりも高速に学習できることが報告されています。
また、これまでベースとしていた強化学習手法であるQ-Learningとは違い、Actor-Criticを採用しています。
主な特徴は以下の2点です。
- Asynchronous
CPUのマルチスレッドで同時に複数のエージェントを並列で走らせ、パラメータを非同期に更新します。
つまり、
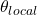 (スレッドごとに別々のパラメータ)
(スレッドごとに別々のパラメータ) 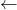
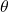 (グローバルなパラメータ)(同期)
(グローバルなパラメータ)(同期)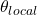 を使って勾配
を使って勾配 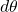 を計算
を計算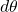 で
で 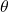 を更新
を更新- 上記を繰り返す
ということをします。
また、この時にパラメータだけでなく、最適化アルゴリズムRMSpropの変数についてもグローバルに共有するようです。
![]()
![]()
- Advantage Actor-Critic
Actor-Criticは、政策 ![]() と、状態価値関数
と、状態価値関数 ![]() をそれぞれ独立に推定しながら学習を行う強化学習手法です。
をそれぞれ独立に推定しながら学習を行う強化学習手法です。
それぞれ独立に行うことにより、行動が連続的な場合でも学習させやすいといったメリットがあります。
ただし、状態価値関数は、報酬 ![]() と次の状態価値
と次の状態価値 ![]() を使って更新されます。
を使って更新されます。
したがって、次の状態価値が正しくなければ、現在の状態価値も正しく推定されないといった問題も起こります。
そこで、Actor-Criticによって時系列にまま学習できる性質を生かし、![]() ステップ先までの報酬を考慮した推定値(Advantage)を使います。
ステップ先までの報酬を考慮した推定値(Advantage)を使います。
これにより、現在の状態価値が、より確からしい推定値となり、学習が早く進むようです。
これらの工夫によって、これまでのDQNよりも学習速度が大幅に向上することが以下のように報告されています。
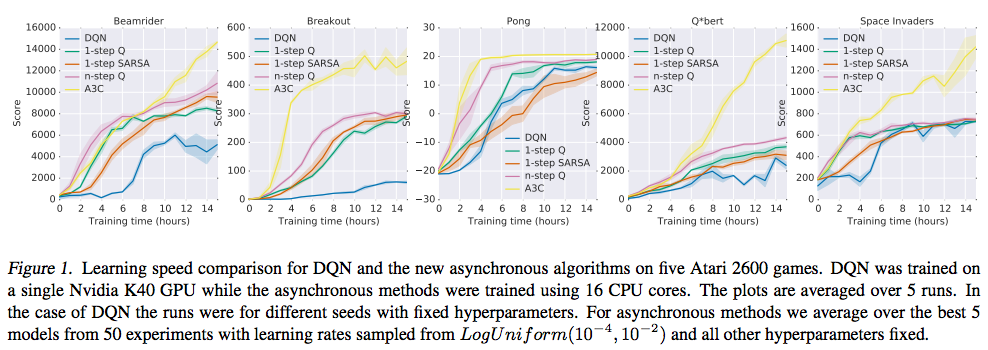
黄色線がA3Cで、青色線がDQNのようですが、Breakoutとか、序盤からでもすぐに学習するようになって、かなり違うように見えます。
まとめ
以上、DQNの実装と、最近のDQN周りの深層強化学習について触れました。
今回の紹介はここまでとなりますが、2017年になってからは、A3CにおいてもGPUを扱う論文なども出ていますので、興味のある方は見てみると良いと思います。
また、つい先日発売された書籍「速習 強化学習: 基礎理論とアルゴリズム」では、今回紹介したところまでの深層強化学習の手法についても触れていますので、参考になると思います。
深層強化学習はむしろ付録であって、強化学習の歴史的な発展について、詳しく解説されている書籍ですので、強化学習の勉強におすすめな本です。
今後は、個人的には、A3Cなどもいずれは実装してみて、中身について深く理解してみたいです。
また、A3Cのアルゴリズムについては、実は、深層強化学習のライブラリとして公開されている「ChainerRL」に、すでに実装されています。
ChainerRL: https://github.com/chainer/chainerrl
単純に学習を試したいというのであれば、こちらを試してみるのも良いかもしれません。

コメント