表題の通り、画像データセットから自己符号化器で特徴を学習し、類似度を測ってみました。
データセットはKaggleからお借りし、ライブラリはTensorFlowを使いました。
画像処理と自己符号化器、そしてTensorFlowの勉強のためにやってみました。
自己符号化器(オートエンコーダ)
下記、Wikipediaより引用です。
オートエンコーダ(自己符号化器、英: autoencoder)とは、機械学習において、ニューラルネットワークを使用した次元圧縮のためのアルゴリズム。
何番煎じといったところなので説明も今更ですが、3層のニューラルネットワークを構築し、中間層を圧縮したい次元数に設定します。
その上で、入力値と出力値が同じデータの値になるように教師あり学習をさせることで、中間層の重みを更新するといった手法になります。
これにより、中間層はデータの次元よりも少ない次元で特徴を表現することになります。
※自己符号化器(オートエンコーダ)のイメージ(Wikipediaオートエンコーダより)
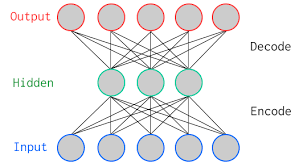
ちなみに次元圧縮の手法としては、主成分分析が定番かと思いますが、自己符号化器と主成分分析にも関係があったりします。
詳しい説明は省略しますが、中間層の活性化関数を恒等写像にした場合には、自己符号化器と主成分分析は同じ働きをします。
したがって、非線形性を加味することによりデータをうまく表現できることが期待できるのであれば、自己符号化器を使うことを検討するのもアリと解釈すれば良いと思います。
データセット
Kaggleで公開されているデータセットを利用します。
Kaggleは、データ分析のコンペティションサイトで、世界中のデータサイエンティスト達が分析スキルを競い合うことができるサイトです。
また、Kaggleではユーザーが集めたデータセットを公開することができます。
特に何か予測モデルを作って欲しいという目的はないので競い合うといったことにはなりませんが、ネタとして「こんなデータがあったとしたら、こんなことをしてみたい」と考えた時に、オープンデータを検索するような感覚で、探して使うことができます。
今回はそのデータセットの中で見つけた、下記の花の画像データセットを使ってみます。
Flower Color Images: https://www.kaggle.com/olgabelitskaya/flower-color-images
下記のような、花の写真の画像が約200枚格納されています。
import glob
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pylab as plt
matplotlib.style.use("ggplot")
import tensorflow as tf
from tqdm import tqdm
import cv2
org_x, train_x = [], []
for path in tqdm(glob.glob('./flower_images/*.png')):
img = cv2.imread(path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
org_x.append(img)
img = cv2.resize(img, (100, 100))
train_x.append(img)
train_x = np.array(train_x, dtype='float32')
plt.imshow(train_x[0].astype('uint8'), cmap='gray', vmin=0, vmax=255, interpolation='none')
plt.show()

TensorFlowによる実装
さて、今回はこのデータセットを自己符号化器で学習して、圧縮した特徴量の類似度から、似たような花を提示することができるかを実装してみます。
コードの全文は下記のGitHubにあげています。
移設しました。
ネットワークをTensorFlowで構築し、学習させるコードが下記になります。
s = train_x.shape
flatten_size = s[1]*s[2]*s[3]
train_x2 = train_x.reshape(len(train_x), flatten_size)
N = len(train_x2)
x_ = tf.placeholder(tf.float32, shape=(None, flatten_size))
h_size = 50
w_enc = tf.Variable(tf.random_normal([flatten_size, h_size], mean=0.0, stddev=0.05), dtype=tf.float32)
b_enc = tf.Variable(tf.random_normal([h_size], mean=0.0, stddev=0.05), dtype=tf.float32)
enc = tf.nn.softsign(tf.matmul(x_, w_enc) + b_enc)
w_dec = tf.Variable(tf.random_normal([h_size, flatten_size], mean=0.0, stddev=0.05), dtype=tf.float32)
b_dec = tf.Variable(tf.random_normal([flatten_size], mean=0.0, stddev=0.05), dtype=tf.float32)
dec = tf.nn.relu(tf.matmul(enc, w_dec)+b_dec)
loss = tf.nn.l2_loss(dec-x_)
train_step = tf.train.AdamOptimizer().minimize(loss)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
EPOCH_NUM = 500000
BATCH_SIZE = 100
for epoch in tqdm(range(EPOCH_NUM)):
perm = np.random.permutation(N)
total_loss = 0
for i in range(0, N, BATCH_SIZE):
batch_x = train_x2[perm[i:i+BATCH_SIZE]]
total_loss += loss.eval(session=sess, feed_dict={x_: batch_x})
train_step.run(session=sess, feed_dict={x_: batch_x})
if (epoch+1) % 1000 == 0:
print("epoch:\t{}\ttotal loss:\t{}".format(epoch+1, total_loss))
学習が終了した後に、実際にちゃんとデコードができているか、いくつかの画像をサンプリングして確認してみます。
sample = np.random.randint(0, N, 10)
for i in sample:
fig, axs = plt.subplots(ncols=3, figsize=(15,3))
axs[0].imshow(org_x[i], cmap='gray', vmin=0, vmax=255, interpolation='none')
axs[0].set_title('org')
axs[1].imshow(train_x[i].reshape(s[1], s[2], s[3]).astype('uint8'), cmap='gray', vmin=0, vmax=255, interpolation='none')
axs[1].set_title('x')
d = dec.eval(session=sess, feed_dict={x_: train_x2[i].reshape(1,flatten_size)})
axs[2].imshow(d.reshape(s[1], s[2], s[3]).astype('uint8'), cmap='gray', vmin=0, vmax=255, interpolation='none')
axs[2].set_title('dec')
plt.show()
e = enc.eval(session=sess, feed_dict={x_: train_x2[i].reshape(1,flatten_size)})
print("enc")
print(e)



左から、org が取り込んだオリジナルの画像、x はリサイズ等を加えた後にネットワークに入力する時のデータの画像、dec がネットワークの出力値の画像です。
encが中間層の値なので、これがエンコードの値となります。
結果として、一部学習しきれていない画像もありましたが、ある程度はデコードできるところまで学習しているようです。
エンコードの値がやたら振り切れているのも気になりますが、ひとまずはこのまま突っ切ってみます。
いくつかのサンプル画像を抽出してきて、エンコードの値で類似度を測ってみます。
今回はコサイン類似度を測ってみて、類似度が高いものを並べて表示してみました。
sample = np.random.randint(0, N, 10)
for i in sample:
e1 = enc.eval(session=sess, feed_dict={x_: train_x2[i].reshape(1,flatten_size)})
e2 = enc.eval(session=sess, feed_dict={x_: train_x2})
e1_ = tf.placeholder(tf.float32, shape=[None, None])
e2_ = tf.placeholder(tf.float32, shape=[None, None])
normalize_e1 = tf.nn.l2_normalize(e1_,1)
normalize_e2 = tf.nn.l2_normalize(e2_,1)
cos_similarity = tf.reduce_sum(tf.multiply(normalize_e1, normalize_e2), axis=1)
tmp_sess = tf.Session()
d = cos_similarity.eval(session=tmp_sess, feed_dict={e1_: e1, e2_: e2})
idxs = np.argsort(d)[::-1]
idxs = np.delete(idxs, np.where(idxs==i))
sim_num = 3
idxs = idxs[:sim_num]
fig, axs = plt.subplots(ncols=4, figsize=(15, sim_num))
axs[0].imshow(train_x2[i].reshape(s[1], s[2], s[3]).astype('uint8'), cmap='gray', vmin=0, vmax=255, interpolation='none')
axs[0].set_title('target')
for k in range(sim_num):
axs[k+1].imshow(train_x2[idxs[k]].reshape(s[1], s[2], s[3]).astype('uint8'), cmap='gray', vmin=0, vmax=255, interpolation='none')
axs[k+1].set_title(str(d[idxs[k]]))
plt.show()
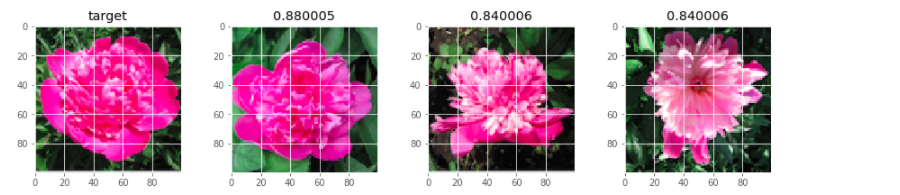
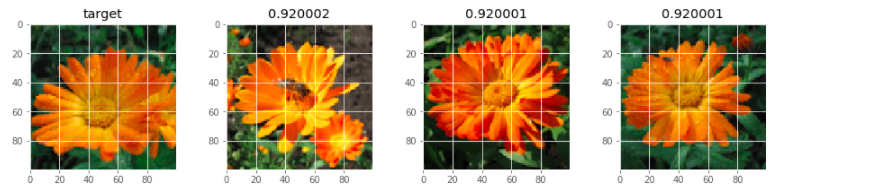
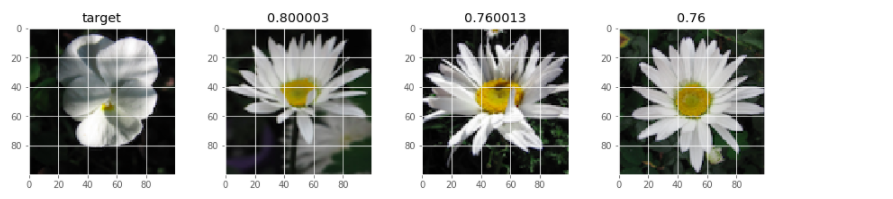
サンプリングしてきた画像のエンコード値と、他のすべての画像のエンコード値を計算し、コサイン類似度を計算しています。
類似度の高いものを上から3つ取って、大きい画像を類似度と一緒に並べて出してみました。
こうしてみると、割りとうまくいっているように見えます。
まとめ
以上、TensorFlowで自己符号化器の実装を行ってみました。
学習が少しばかり足りていなさそうでしたので、もう少し学習させれば、色だけでなく形も似ているものを抽出してきてくれそうな気がしました。
といっても、画像データすべて確認しているわけではないので、理想的にこれ!って答えがあるわけではないのですが...。
また、エンコードの値であってもなくても、全ての画像データと類似度を測るのは時間がかかるのではないかとも思われるかもしれませんが、一度学習してしまえば、自己符号化器の推論は予想以上に早く、類似度計算も割とすぐにレスポンスを返してくれました。
こういった点から、対話的操作が求められるようなシステムの導入などに利点がありそうな気がしました。
追記(2017-12-16)
同じデータセットで、転移学習による類似度計算も試してみました。

コメント