スポンサーリンク

ベイジアンニューラルネットワークで毒キノコ分類を実装してみた

Edward Python データ分析 ベイジアンモデル 機械学習

最近勉強中のEdwardを使って、ベイジアンニューラルネットワークを実装してみました。

公式ページには、ちょっとした参考程度にしかコードが書いてなくて、自信はありませんが、とりあえず学習はしてくれたようです。

ちなみに今回は、データをKaggleのデータセットで行い、実装もKaggleのkernelを使ってみました。

Bayesian Neural Network with Edward: https://www.kaggle.com/itoeiji/bayesian-neural-network-with-edward

Kaggleのkernel環境のDockerファイルなどを確認してみましたが、ほとんどのPythonのライブラリが入っていて、今回のEdwardも含まれていました。

上記とは別で下記GitHubにもあげています。

GitHub: https://github.com/Gin04gh/datascience/blob/master/kaggle_dataset_mushroom_classification/bayesian_neural_network_edward.ipynb

ベイズ推論

ベイズ推論では、観測データの集合 \mathcal{D} と未知のパラメータ \theta に関して、モデル p(\mathcal{D},\theta)=p(\mathcal{D}|\theta)p(\theta) を構築し、事後分布

    \[p(\theta|\mathcal{D})=\frac{p(\mathcal{D}|\theta)p(\theta)}{p(\mathcal{D})}=\frac{p(\mathcal{D}|\theta)p(\theta)}{{\int}p(\mathcal{D}|\theta)p(\theta)d\theta}\]

を解析的または近似的に求めます。

モデルの構築において、自然共益事前分布を仮定すれば、事後分布は解析的に求まりますが、そうでない場合は、 {\int}p(\mathcal{D}|\theta)p(\theta)d\theta の計算がとても困難なものになるため、代わりにマルコフ連鎖モンテカルロ法や変分推論を使って、近似的に事後分布を求めます。

マルコフ連鎖モンテカルロ法（Markov Chain Monte Carlo; MCMC）では、 \theta_i{\sim}p(\theta|\mathcal{D}) を大量に得て（サンプリング）、平均や分散を求めてみたり、プロットしてみたりして、分布の外観を把握します。

変分推論（Variational Inference）（または変分近似（Variational Approximation））では、解析しやすい分布 q({\theta};\eta) を考え、p(\theta|\mathcal{D}){\approx}q({\theta};\eta) と近似します。

言い換えると、目的関数　\arg\min_{\eta}KL(q({\theta};\eta}){\parallel}p(\theta|\mathcal{D})) の最小化問題を解くことになります。

実際にどのようにしてサンプリングや近似をさせるのかといった話は、今回に関してはEdwardがライブラリとしてやってくれる話なので、省略します。（というか勉強中です...）

書籍としては、最近出版されたものとしては、下記などが参考になると思います。

ベイズ推論による機械学習入門（機械学習スタートアップシリーズ）
須山敦志、杉山将

上記書籍はサンプルコードもGitHubに上がっています。（ただし、juliaです笑）

- https://github.com/sammy-suyama/BayesBook

ベイジアンニューラルネットワーク

ベイジアンニューラルネットワークでは、ニューラルネットワークのパラメータ \boldsymbol{w} （重みとバイアス）が、ある確率分布に従うと仮定し、その事後分布をベイズ推論により求めます。

    \[\boldsymbol{w}{\sim}\mathcal{N}(\boldsymbol{0}, \boldsymbol{\text{I}})\]

    \[p(y|\boldsymbol{x},\boldsymbol{w})=\text{Categorical}\left(\frac{\exp(f(\boldsymbol{x},\boldsymbol{w}))}{\Sigma\exp(f(\boldsymbol{x},\boldsymbol{w}))}\right)\]

（ここでいう f({\cdot}) は活性化関数などを表します）

ニューラルネットワークにベイジアンを適用する話は、歴史的には結構古くからあったようで、メリットやデメリットとしては下記のように、やはりベイズ推論で一般的によく言われることと同等のことが言えるようです。

メリット デメリット
・ 少ない学習データで学習が可能
・ 過学習が抑えられる（というか過学習という概念がない） 		・ 計算量が多い
・ 再現性がない場合がある

Edward

Edwardはベイズ統計などで扱うような確率モデルを実装できるライブラリです。

同じPythonのライブラリで言えば、PyStanやPyMCがその類のものになります。

Edward: http://edwardlib.org/

特徴としては、

  • 2016年より開発されている確率的プログラミングのPythonライブラリ
  • Dustin Tran氏(Open AI)が開発をリード
  • LDAで有名なコロンビア大学のBlei先生の研究室で開発
  • 計算にTensorFlowを用いている
  • 計算速度がStanやPyMC3よりも速い
  • GPUによる高速化が可能
  • TensorBoardによる可視化も可能

などが挙げられます。

ベイズ統計はもちろんですが、深層学習などに対するベイズの適用の実装も可能のようです。

この辺りについてはチュートリアルに色々と参考例があり、例えば、下記のようなアルゴリズムの実装が可能のようです。

また、現段階において、TensorFlowにマージされる予定のようです。

参考: https://discourse.edwardlib.org/t/edward-is-officially-moving-into-tensorflow/387

ちなみにこの「Edward」という名前については、統計学者のGeorge Edward Pelham Boxから取っているようです。

Box-Cox変換やLjung-Box検定のBoxだったかと思います。

Edwardの使い方

EdwardはバックエンドにTensorFlowを用いており、使い勝手もTensorFlowと同様に、計算グラフを作成、セッションを宣言、値をフローという流れで使用します。

import numpy as np
import tensorflow as tf
import edward as ed

# 正規分布の値を生成
from edward.models import Normal

x = Normal(loc=0.0, scale=1.0)
sess = tf.Session() # or ed.get_session()
sample_x = sess.run(x)
print(sample_x)
# 0.0919603

テンソルで処理できるため、一気に値をベクトル生成することも可能です。

# テンソルで生成可能
from edward.models import Normal

N = 10
x = Normal(loc=tf.zeros([N]), scale=tf.ones([N]))
sess = tf.Session() # or ed.get_session()
samples_x = sess.run(x)
print(samples_x)
# [-0.36161533 -0.67601579 -1.04770219 -0.70425886 -0.62890649  0.3660461
#  0.31013817 -0.64070946  0.26981813  0.24564922]

パラメータの事前分布を指定する場合も、以下のようにPythonっぽく書けます。

この辺りはStanなどよりもPyMCと似ています。

# 正規分布の平均が正規分布に従うモデルの値を生成
from edward.models import Normal

mu = Normal(loc=0.0, scale=1.0)
x = Normal(loc=mu, scale=1.0)
sess = tf.Session()
sample_mu, sample_x = sess.run([mu, x])
print(sample_mu)
print(sample_x)
# -0.622465
# 1.9574

もちろん計算グラフなので、プレースホルダーを用いて、値を供給して生成することもできます。

# 変数に値を供給して値を生成
from edward.models import Normal

mu_ = tf.placeholder(tf.float32)
x = Normal(loc=mu_, scale=1.0, sample_shape=10)
sess = tf.Session()
mu, samples_x = sess.run([mu_, x], feed_dict={mu_: 50.0})
print(mu)
print(samples_x)
# 50.0
# [ 49.63046646  47.55083084  49.45754623  49.77397919  51.31248474
#  48.98104858  52.11248398  50.42101669  50.32041931  50.07067108]

パラメータの事後分布を求める場合には、変分推論かMCMC法が使えます。

# 正規分布のパラメータの事後分布を求める（変分推論）
from edward.models import Normal

N = 30
x_train = np.random.randint(10, 20, N) # 10〜20の観測値がN個
mu = Normal(loc=0.0, scale=1.0)
x = Normal(loc=mu, scale=1.0, sample_shape=N)
qmu = Normal(loc=tf.Variable(0.0), scale=1.0)
inference = ed.KLqp({mu: qmu}, data={x: x_train})
inference.run(n_iter=1000)
samples = qmu.sample(100).eval()
print(samples.mean())
# 1000/1000 [100%] ██████████████████████████████ Elapsed: 0s | Loss: 278.396
# 14.7295

# 正規分布のパラメータの事後分布を求める（MCMC）
from edward.models import Empirical

N = 30
x_train = np.random.randint(10, 20, N) # 10〜20の観測値がN個
T = 1000
mu = Normal(loc=0.0, scale=1.0)
x = Normal(loc=mu, scale=1.0, sample_shape=N)
qmu = Empirical(tf.Variable(tf.zeros(T)))
inference = ed.HMC({mu: qmu}, {x: x_train})
inference.run(n_iter=T)
samples = qmu.sample(100).eval()
print(samples.mean())
# 1000/1000 [100%] ██████████████████████████████ Elapsed: 1s | Acceptance Rate: 0.915
# 14.7666

今回扱うデータについて

上記説明の通り、Kaggleのデータセットページからkernelを作成して実装しています。

- https://www.kaggle.com/itoeiji/bayesian-neural-network-with-edward

今回は食用キノコと毒キノコの分類用データセットです。

mushrooms.csvを見てみると下記のようになっています。

data = pd.read_csv('../input/mushrooms.csv')
data.head()

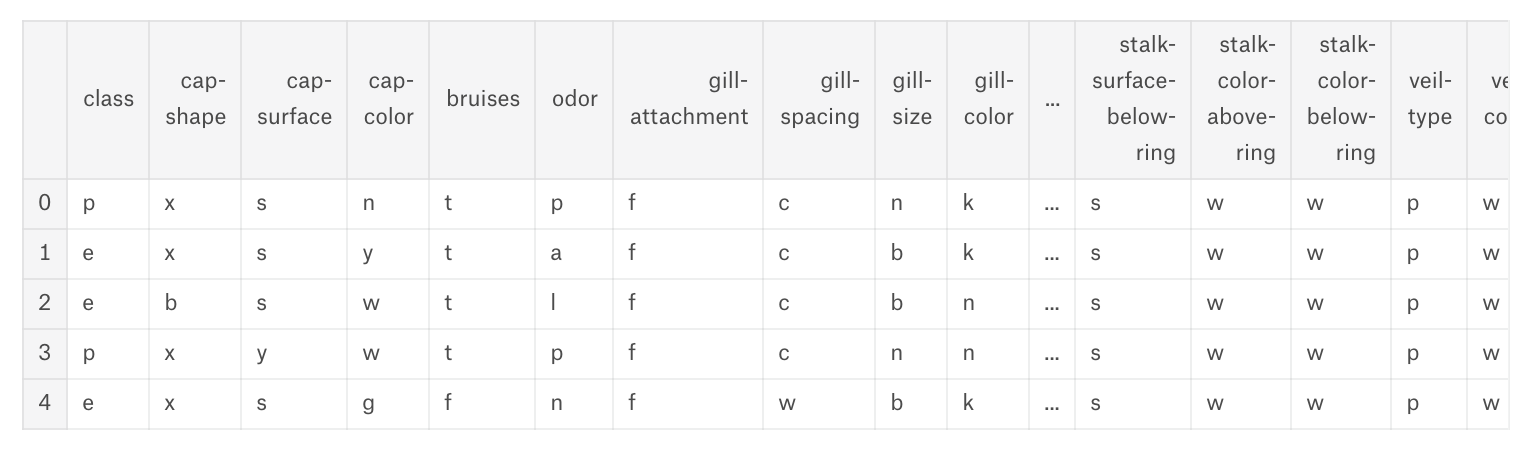
一番左のclass列がpが毒（poisson）、eが食用（eatable）となっているようです。

カラムは全てオブジェクト型のようなので、ダミー変数化しておきます。

data2 = pd.get_dummies(data)
data2.shape

カラムが目的変数分の2カラムを引いて、117カラムあるようなので、これを全て説明変数ベクトルとして与えて、ニューラルネットワークを解いてみます。

ベイジアンニューラルネットワークの実装

まずは教師データを準備します。

上記のように、class_pとclass_eはラベルデータで、残りを入力データとします。

data_x = data2.loc[:, 'cap-shape_b':].as_matrix().astype(np.float32)
data_y = data2.loc[:, :'class_p'].as_matrix().astype(np.float32)

N = 7000
train_x, test_x = data_x[:N], data_x[N:]
train_y, test_y = data_y[:N], data_y[N:]

in_size = train_x.shape[1]
out_size = train_y.shape[1]

EPOCH_NUM = 5
BATCH_SIZE = 1000

# for bayesian neural network
train_y2 = np.argmax(train_y, axis=1)
test_y2 = np.argmax(test_y, axis=1)

まずは簡単に比較のため、隠れ層のない単純なニューラルネットワークを、TensorFlowで構築して、学習させてみます。

import sys
from tqdm import tqdm
import tensorflow as tf

x_ = tf.placeholder(tf.float32, shape=[None, in_size])
y_ = tf.placeholder(tf.float32, shape=[None, out_size])
w = tf.Variable(tf.truncated_normal([in_size, out_size], stddev=0.1), dtype=tf.float32)
b = tf.Variable(tf.constant(0.1, shape=[out_size]), dtype=tf.float32)
y_pre = tf.matmul(x_, w) + b

cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_pre))
train_step = tf.train.AdamOptimizer().minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_pre, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for epoch in tqdm(range(EPOCH_NUM), file=sys.stdout):
    perm = np.random.permutation(N)

    for i in range(0, N, BATCH_SIZE):
        batch_x = train_x[perm[i:i+BATCH_SIZE]]
        batch_y = train_y[perm[i:i+BATCH_SIZE]]
        train_step.run(session=sess, feed_dict={x_: batch_x, y_: batch_y})

    acc = accuracy.eval(session=sess, feed_dict={x_: train_x, y_: train_y})
    test_acc = accuracy.eval(session=sess, feed_dict={x_: test_x, y_: test_y})

    if (epoch+1) % 1 == 0:
        tqdm.write('epoch:\t{}\taccuracy:\t{}\tvaridation accuracy:\t{}'.format(epoch+1, acc, test_acc))

問題なく学習できているようです。

どうでも良いですが、validationがvaridationと綴を間違っていました。（この後のコードも間違ったままですが、目を瞑ってください）

次に、ベイジアンニューラルネットワークをEdwardで構築して、学習させてみます。

import edward as ed
from edward.models import Normal, Categorical

x_ = tf.placeholder(tf.float32, shape=(None, in_size))
y_ = tf.placeholder(tf.int32, shape=(BATCH_SIZE))
w = Normal(loc=tf.zeros([in_size, out_size]), scale=tf.ones([in_size, out_size]))
b = Normal(loc=tf.zeros([out_size]), scale=tf.ones([out_size]))
y_pre = Categorical(tf.matmul(x_, w) + b)

qw = Normal(loc=tf.Variable(tf.random_normal([in_size, out_size])), scale=tf.Variable(tf.random_normal([in_size, out_size])))
qb = Normal(loc=tf.Variable(tf.random_normal([out_size])), scale=tf.Variable(tf.random_normal([out_size])))
y = Categorical(tf.matmul(x_, qw) + qb)

inference = ed.KLqp({w: qw, b: qb}, data={y_pre: y_})
inference.initialize()

sess = tf.Session()
sess.run(tf.global_variables_initializer())

with sess:
    samples_num = 100

    for epoch in tqdm(range(EPOCH_NUM), file=sys.stdout):
        perm = np.random.permutation(N)

        for i in range(0, N, BATCH_SIZE):
            batch_x = train_x[perm[i:i+BATCH_SIZE]]
            batch_y = train_y2[perm[i:i+BATCH_SIZE]]
            inference.update(feed_dict={x_: batch_x, y_: batch_y})

        y_samples = y.sample(samples_num).eval(feed_dict={x_: train_x})
        acc = (np.round(y_samples.sum(axis=0) / samples_num) == train_y2).mean()

        y_samples = y.sample(samples_num).eval(feed_dict={x_: test_x})
        test_acc = (np.round(y_samples.sum(axis=0) / samples_num) == test_y2).mean()

        if (epoch+1) % 1 == 0:
            tqdm.write('epoch:\t{}\taccuracy:\t{}\tvaridation accuracy:\t{}'.format(epoch+1, acc, test_acc))

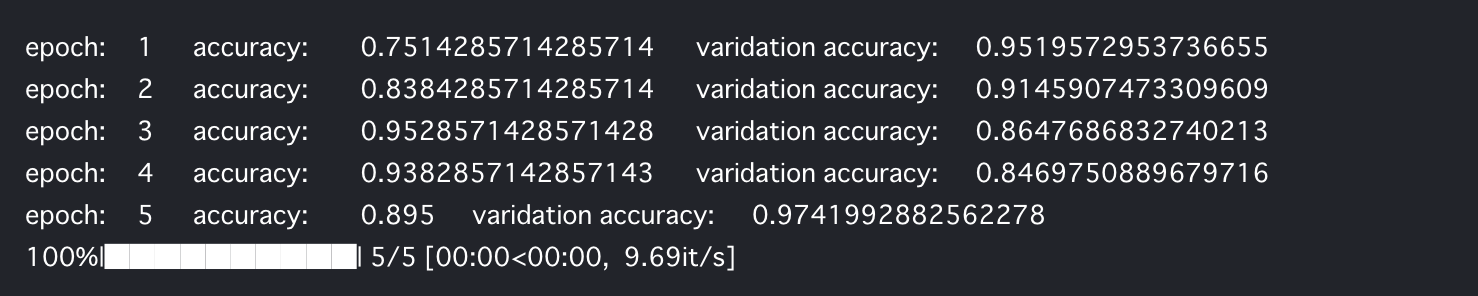
こちらも学習できたようです。

注意する点としては、仮定した分布を使って予測する計算グラフ y_pre とラベルデータ y_ が一致するよう inference で設定する点と、精度確認のための、近似させた分布を使って予測する計算グラフ y を用意しておくところなどでしょうか。

また、各ニューロンが確率分布になるので、同じデータを x_ に与えたとしても、予測結果 y　は当然確率によって値が変動します。

そのため、精度を確認する際には、ある程度、同じデータを与えてサンプリングを行い、どちらのラベルである確率が高いかを見て判断させています。

y_samples = y.sample(samples_num).eval(feed_dict={x_: train_x})
acc = (np.round(y_samples.sum(axis=0) / samples_num) == train_y2).mean()

y_samples = y.sample(samples_num).eval(feed_dict={x_: test_x})
test_acc = (np.round(y_samples.sum(axis=0) / samples_num) == test_y2).mean()

がその箇所になります。

一応これで何かしら精度が上がったことが確認できました。

ニューラルネットワークと同様にエポックを回してみましたが、序盤から割りと精度が高く、むしろエポックを重ねて精度が上がるかというと、そうでもないし、ベイジアン的に考えたら、あまり意味がないようにも思いますが、実際どうなのでしょうか。

さらに興味がある点としては、今回は隠れ層なしでしたけども、隠れ層を入れた場合には、同じような作りで良いのかも気になるところです。

動かしてみたら、返って謎が深まってしまった感じがしますが、今回はひとまず、ここまでとしておきます。

スポンサーリンク

コメント