今回は数理最適化問題を深層強化学習で解くアプローチについて書きます。
前回、巡回セールスマン問題(TSP)について、混合整数計画問題(MIP)としての解き方をPuLPで実装しました。

今回は、TSPについて深層強化学習を使った解き方をPyTorchで試してみます。
実はこちらは結構以前に試したのですが、ここに書き記す時間がなかなか取れず、だいぶ暖めてしまいました。
結果、当時の思考をあまり思い出せないところも幾分かあり、なので今回はざっくりなご紹介といった記事になります。
ソースコードは当時から残っていたものがフルでありますので、以下のいずれかよりご参照下さい。
kaggle notebook: https://www.kaggle.com/itoeiji/tsp-pulp-optimization-pytorch-deep-learning
巡回セールスマン問題(Traveling Salesman Problem; TSP)
TSPは、ある都市から出発し、全ての都市を訪れて元の都市に戻ることを考えた時に、総移動距離が一番最短となるルートを求める最適化問題で、組み合わせ最適化問題の中でも代表的な問題の1つで、NP困難と呼ばれる問題のクラスに属します。
詳しくは過去の記事を参照していただければと思います。
一般的にはこういった問題は前回記事のように最適化手法を用いて解きます。
一方で、近年では、ニューラルネットワークや深層学習が発展したことにより、深層強化学習を使ったアプローチ手法も提案されたりしています。
そのような手法を使う場合はどのような実装になり、どのような効果がありそうか試してみましたので、それについて記します。
深層強化学習によるアプローチについて
深層学習モデルのアーキテクチャはPointer Networkと呼ばれるモデルを試しました。
Pointer Networks: https://arxiv.org/abs/1506.03134
Pointer Networkは2017年にGoogleが出した論文で提案されたモデルであり、その少し前に登場したばかりのSeq2Seqから派生したモデルです。
予測・出力のイメージはSeq2Seqと同様に、入力シーケンスと出力シーケンスがあり、TSPにおいては、入力は単に都市のポイント列を入力して都市位置情報を与え、予測においては巡回する都市ポイントの列を出力します。
これにPtr-Netと呼ばれる機構を導入する工夫がなされており、(あまり覚えていませんが)入力ポイントを直接参照するAttentionに近い機構で都市を重複して回らないようにします。
実装は以下ような感じ。
class Attention(nn.Module):
def __init__(self, hidden_size, use_tanh=False, C=10, use_cuda=use_cuda):
super(Attention, self).__init__()
self.use_tanh = use_tanh
self.C = C
# Bahdanau algo
self.W_query = nn.Linear(hidden_size, hidden_size)
self.W_ref = nn.Conv1d(hidden_size, hidden_size, 1, 1)
V = torch.cuda.FloatTensor(hidden_size) if use_cuda else torch.FloatTensor(hidden_size)
self.V = nn.Parameter(V)
self.V.data.uniform_(-(1. / math.sqrt(hidden_size)) , 1. / math.sqrt(hidden_size))
def forward(self, query, ref):
# query = [batch_size, hidden_size]
# ref = [batch_size, seq_len, hidden_size]
batch_size = ref.size(0)
seq_len = ref.size(1)
# Bahdanau algo
ref = ref.permute(0, 2, 1)
query = self.W_query(query).unsqueeze(2) # [batch_size x hidden_size x 1]
ref = self.W_ref(ref) # [batch_size x hidden_size x seq_len]
expanded_query = query.repeat(1, 1, seq_len) # [batch_size x hidden_size x seq_len]
V = self.V.unsqueeze(0).unsqueeze(0).repeat(batch_size, 1, 1) # [batch_size x 1 x hidden_size]
logits = torch.bmm(V, torch.tanh(expanded_query + ref)).squeeze(1)
if self.use_tanh:
logits = self.C * torch.tanh(logits)
return ref, logits
class GraphEmbedding(nn.Module):
def __init__(self, input_size, embedding_size, use_cuda=use_cuda):
super(GraphEmbedding, self).__init__()
self.embedding_size = embedding_size
self.use_cuda = use_cuda
self.embedding = nn.Parameter(torch.FloatTensor(input_size, embedding_size))
self.embedding.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))
def forward(self, inputs):
# inputs = [batch_size, input_size, seq_len]
batch_size = inputs.size(0)
seq_len = inputs.size(2)
embedding = self.embedding.repeat(batch_size, 1, 1)
embedded = []
inputs = inputs.unsqueeze(1)
for i in range(seq_len):
embedded.append(torch.bmm(inputs[:, :, :, i].float(), embedding))
embedded = torch.cat(embedded, 1)
return embedded
class PointerNet(nn.Module):
def __init__(self, embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, use_cuda=use_cuda):
super(PointerNet, self).__init__()
self.embedding_size = embedding_size
self.hidden_size = hidden_size
self.n_glimpses = n_glimpses
self.seq_len = seq_len
self.use_cuda = use_cuda
self.embedding = GraphEmbedding(2, embedding_size, use_cuda=use_cuda)
self.encoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
self.decoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
self.pointer = Attention(hidden_size, use_tanh=use_tanh, C=tanh_exploration, use_cuda=use_cuda)
self.glimpse = Attention(hidden_size, use_tanh=False, use_cuda=use_cuda)
self.decoder_start_input = nn.Parameter(torch.FloatTensor(embedding_size))
self.decoder_start_input.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))
def apply_mask_to_logits(self, logits, mask, idxs):
batch_size = logits.size(0)
clone_mask = mask.clone()
if idxs is not None:
clone_mask[[i for i in range(batch_size)], idxs.data] = 1
logits[clone_mask] = -np.inf
return logits, clone_mask
def forward(self, inputs):
# inputs = [batch_size, 1, seq_len]
batch_size = inputs.size(0)
seq_len = inputs.size(2)
embedded = self.embedding(inputs)
encoder_outputs, (hidden, context) = self.encoder(embedded)
prev_probs = []
prev_idxs = []
mask = torch.zeros(batch_size, seq_len).byte().cuda() if self.use_cuda else torch.zeros(batch_size, seq_len).byte()
idxs = None
decoder_input = self.decoder_start_input.unsqueeze(0).repeat(batch_size, 1)
for i in range(seq_len):
_, (hidden, context) = self.decoder(decoder_input.unsqueeze(1), (hidden, context))
query = hidden.squeeze(0)
for i in range(self.n_glimpses):
ref, logits = self.glimpse(query, encoder_outputs)
logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
query = torch.bmm(ref, F.softmax(logits).unsqueeze(2)).squeeze(2)
_, logits = self.pointer(query, encoder_outputs)
logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
probs = F.softmax(logits)
idxs = probs.multinomial(num_samples=1).squeeze(1)
for old_idxs in prev_idxs:
if old_idxs.eq(idxs).data.any():
idxs = probs.multinomial(num_samples=1).squeeze(1)
break
decoder_input = embedded[[i for i in range(batch_size)], idxs.data, :]
prev_probs.append(probs)
prev_idxs.append(idxs)
return prev_probs, prev_idxs
さて、学習の方法なのですが、前述のPointer Networksの論文の中でもTSPへの応用は言及されていますが、その時は最適化手法による解を教師データとして学習させていました。
一方で、下記論文にて、深層強化学習の枠組みで考えることで、探索的に最適巡回路を求める学習方法が提案されています。
Neural Combinatorial Optimization with Reinforcement Learning: https://arxiv.org/abs/1611.09940
強化学習アーキテクチャは論文内の以下の通りです。

ここで報酬は負の総移動距離とし、ポリシーで提案した移動の順番の総移動距離が短くなればなるほど報酬が上がっていくようにしています。
実装は以下のような感じ。
def reward(sample_solution, use_cuda=use_cuda):
batch_size = sample_solution[0].size(0)
n = len(sample_solution) # sample_solution is seq_len of [batch_size]
tour_len = Variable(torch.zeros([batch_size])).cuda() if use_cuda else Variable(torch.zeros([batch_size]))
for i in range(n - 1):
tour_len += torch.norm(sample_solution[i] - sample_solution[i + 1], dim=1)
tour_len += torch.norm(sample_solution[n - 1] - sample_solution[0], dim=1)
return tour_len
class NeuralCombinatorialOptimization(nn.Module):
def __init__(self, embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, reward, use_cuda=use_cuda):
super(NeuralCombinatorialOptimization, self).__init__()
self.reward = reward
self.use_cuda = use_cuda
self.actor = PointerNet(embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, use_cuda)
def forward(self, inputs):
# inputs = [batch_size, input_size, seq_len]
batch_size = inputs.size(0)
input_size = inputs.size(1)
seq_len = inputs.size(2)
probs, action_idxs = self.actor(inputs)
actions = []
inputs = inputs.transpose(1, 2)
for action_id in action_idxs:
actions.append(inputs[[x for x in range(batch_size)], action_id.data, :])
action_probs = []
for prob, action_id in zip(probs, action_idxs):
action_probs.append(prob[[x for x in range(batch_size)], action_id.data])
R = self.reward(actions, self.use_cuda)
return R, action_probs, actions, action_idxs
実際にTSPを定義して、PuLPで解いてみた場合と比較をしてみます。
TSPの定義およびPuLPの実装に関しては、前回の記事か、冒頭の全体ソースコードを見ていただければと思います。
出発地点を含む都市の数を15として、PuLPで解いてみると、最適解の目的関数は 393 となり、都市の座標および最適なルートは以下のような感じとなりました。
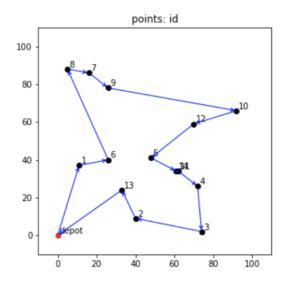
一方で、前述のPointer Networkを用いた深層強化学習で学習させてみました。
学習結果は以下の通りで、最適解であった総移動距離 393 に近い、445 で学習を終えていそうな感じが分かります。

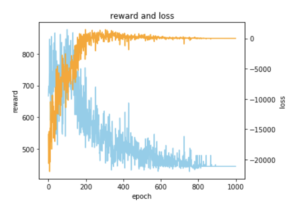
学習させたモデルで最短経路を予測させてみた結果をグラフでプロットしてみると以下のような感じで、最適解にちょっと惜しいようなルートが出てきました。
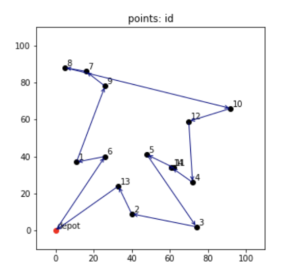
まとめ
個人的にはもっと威力を発揮するのではと思っていたのですが、いまいち有効とは言い切れないような感じだなあと、当時実装結果を見て思った記憶があります。
やはり問題自体の組み合わせ数が闇雲な探索にはハードすぎるのかなと思ったことと、近年発展してきている深層学習や強化学習の効果的な方法をまだあまりこちらの分野に発展し切れていないようにも思いました。
この実装をしていた時にも思いましたが、なぜ入力情報を系列データで入力する必要があったのか分かりませんし。
と思ったら、詳しく調べ切れていませんが、TransformerベースでVRPにアプローチする論文もなんかあるみたいですね。
また、ある程度これよりも大きい規模でかつ条件が頻繁に変わるような(都市座標が毎回変わるみたいな)状態だと、有効な場合もあるのかなと思いました。
最適化手法では毎回解くのに実行時間がかかってしまいますが、このような手法ならランダムに都市情報を変えたトレーニングデータでモデルを長時間学習させたものを持っていれば、毎回推論だけで済むのかなと思います。
そう考えると、学習方法や探索の方法をうまくドメイン的な構造も考慮し発展させていくことができれば、このような組み合わせ最適化問題に対する新しいアプローチも増えていきそうな気がしました。
コメント