表題の通り、数理最適化問題の中でもNP困難の基本的な問題の1つ、巡回セールスマン問題と、その一般化、運搬経路問題を、PuLPで解いてみます。
PuLPは、最適化問題を解くためのPythonライブラリです。
今回は、このライブラリを使って、巡回セールスマン問題および運搬経路問題を、混合整数計画問題として解いてみます。
今回の実装の全コードは以下のいずれかから。
kaggle notebook: https://www.kaggle.com/itoeiji/solving-tsp-and-vrp-by-mip-using-pulp
PuLP
PuLPは、線形計画問題・混合整数計画問題をPythonで定義し、ソルバーを使って解くためのライブラリです。
公式サイトは以下などから。
- https://coin-or.github.io/pulp/index.html
- https://pypi.org/project/PuLP/
- https://github.com/coin-or/pulp
ソルバーは、与えられた制約条件・問題数式に則って、最適解を解析するソフトウェアです。
対して、PuLP自体は最適化問題をモデルする役割を持つため、モデラーと呼ばれたりすることもあります。
PuLPインストール時に同時にデフォルトのソルバーCBCもインストールされ、PuLPで最適化問題を解く時、内部では以下のようなフローが実行されます。
- [PuLPが実行] PuLPで定義した最適化問題を、.mpsファイルとして出力する
- [Solverが実行] .mpsファイルを読み込んで問題を解く
- [Solverが実行] 最適解を.solファイルとして出力する
- [PuLPが実行] .solファイルを読み込んで、最適解を変数に格納する
MPS形式については、以下wikiなども参考。
- https://en.wikipedia.org/wiki/MPS_%28format%29
ソルバーはCBC以外にも、以下のようなツールを別途購入・インストールして、PuLPから使用することができます。
・GLPK(無料)
・SCIP(学術利用無料、商用有料)
・Gurobi(有料)
・CPLEX(有料)
意外とPythonを使った最適化問題の解法に関しては、あまり書籍なども出ていないのですが、以下の書籍は、基本的な最適化問題をPuLPで解くコードが全て載っているので、オススメです。
巡回セールスマン問題(Traveling Salesman Problem; TSP)
巡回セールスマン問題(Traveling Salesman Problem; TSP)とは、ある都市から出発して全ての都市を1度ずつ訪れて、元の都市に戻ることを考えた時に、総移動距離が一番最短となるルートを求める最適化問題です。
組み合わせ最適化問題の代表的な問題の1つで、NP困難と呼ばれる問題のクラスに属します。
都市の数が増えれば増えるほど、組み合わせ候補が爆発的に増えてしまって、計算量的に解析が困難になる問題です。
これを、PuLPを使って、混合整数計画法で解いてみます。
混合整数計画法については、以下のリンクが参考になると思います。
線型計画法よりも、解を探索しづらそうなことが分かりやすですよね。
- https://www.msi.co.jp/nuopt/introduction/algorithm/mip.html
今回の問題となるデータは、以下のようにして自前で作成します。
# define TSP
n_customer = 9
n_point = n_customer + 1
df = pd.DataFrame({
'x': np.random.randint(0, 100, n_point),
'y': np.random.randint(0, 100, n_point),
})
df.iloc[0]['x'] = 0
df.iloc[0]['y'] = 0
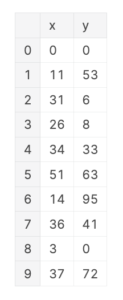
n_customer で都市(訪問するクライアント)の数を設定し、各都市の座標 ![]() を乱数でランダムに振り分けて作成しました。
を乱数でランダムに振り分けて作成しました。
ただし、最初の1点だけは、出発する都市(DEPOT)とします。
DEPOTからスタートして、これらの点を全て経由して、DEPOTに戻る最短経路を求めてみます。
どんな感じの配置関係になっているのかを確認してみると、こんな感じ。
# check TSP state
plt.figure(figsize=(5, 5))
# draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
plt.text(row['x'] + 1, row['y'] + 1, f'{i}')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id')
plt.show()
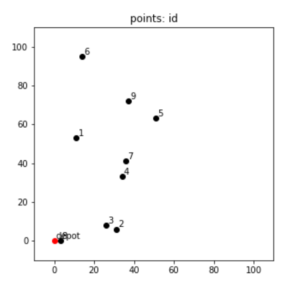
なんかえらく全体的に左側に寄っちゃいましたが、乱数なので仕方がない。(俺くじ運悪いし)
さて、これを解くためのPuLPの実装ですが、コード量は多くないんで、一気に書くと以下のようになります。
# set problem
problem = pulp.LpProblem('tsp_mip', pulp.LpMinimize)
# set valiables
x = pulp.LpVariable.dicts('x', ((i, j) for i in range(n_point) for j in range(n_point)), lowBound=0, upBound=1, cat='Binary')
# we need to keep track of the order in the tour to eliminate the possibility of subtours
u = pulp.LpVariable.dicts('u', (i for i in range(n_point)), lowBound=1, upBound=n_point, cat='Integer')
# set objective function
problem += pulp.lpSum(distances[i][j] * x[i, j] for i in range(n_point) for j in range(n_point))
# set constrains
for i in range(n_point):
problem += x[i, i] == 0
for i in range(n_point):
problem += pulp.lpSum(x[i, j] for j in range(n_point)) == 1
problem += pulp.lpSum(x[j, i] for j in range(n_point)) == 1
# eliminate subtour
for i in range(n_point):
for j in range(n_point):
if i != j and (i != 0 and j != 0):
problem += u[i] - u[j] <= n_point * (1 - x[i, j]) - 1
# solve problem
status = problem.solve()
# output status, value of objective function
status, pulp.LpStatus[status], pulp.value(problem.objective)
"""
(1, 'Optimal', 240.18288657336905)
"""
書き方は自己流かもしれないですけど、問題の宣言・変数の宣言・目的関数の宣言・制約条件を含む定式化のパート別に書いてあります。
![]() が
が ![]() から
から ![]() に移動する場合は1, そうでない場合は0とする決定変数となり、
に移動する場合は1, そうでない場合は0とする決定変数となり、problem += pulp.lpSum(distances[i][j] * x[i, j] for i in range(n_point) for j in range(n_point)) で、![]() の場合にその区間の距離
の場合にその区間の距離 ![]() をかけて総移動距離を計算し、これを最小化しています。
をかけて総移動距離を計算し、これを最小化しています。
また # set constrains のパートでは、同じ都市への移動はありませんので、![]()
都市間の区間は必ず1回だけ通るという制約を入れています。
また # eliminate subtour では、部分巡回経路ができてしまわないように制御しています。
すなわち以下のような状態になってしまわないようにしているということですね。
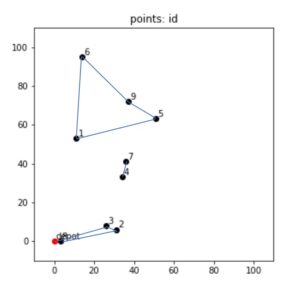
これも確かに、都市間の区間の移動はいずれも1回ですし、同じ都市への移動もないです。
だけど、問題としては巡回して一筆書きのようにしながら最短距離を求めてほしいので、こういった制約を加えます。
以上として問題を解いて、解析実行後のステータス pulp.LpStatus[status] は Optimal で最適解が見つかったという結果となり、最適化された目的関数の値は、 240.18 となりました。
最適化された巡回経路を可視化してみると、以下のような感じ。
# check TSP problem and optimized route
plt.figure(figsize=(5, 5))
# draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
plt.text(row['x'] + 1, row['y'] + 1, f'{i}')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id')
# draw optimal route
routes = [(i, j) for i in range(n_point) for j in range(n_point) if pulp.value(x[i, j]) == 1]
arrowprops = dict(arrowstyle='->', connectionstyle='arc3', edgecolor='blue')
for i, j in routes:
plt.annotate('', xy=[df.iloc[j]['x'], df.iloc[j]['y']], xytext=[df.iloc[i]['x'], df.iloc[i]['y']], arrowprops=arrowprops)
plt.show()
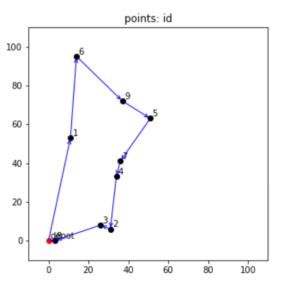
一番頑張ったのは、Matplotlibで矢印を描くところだったと言っても過言ではない←
上記のような回り方で、総移動距離が 240.18 といった感じです。
運搬経路問題(Vehicle Routing Problem; VRP)
運搬経路問題(Vehicle Routing Problem; VRP)はTSPの一般化問題の一種で、複数の車両で複数の顧客のいる場所に訪れ、荷物の集荷or配達をするときに、その総移動距離を最小化するような経路を求める問題です。
巡回セールスマン問題の時よりも、少し実用的な問題に昇格した感じがする一方で、このような運搬経路を実用的な観点で考えると、他にも様々な制約条件が想像できます。
VRPの種類:
| 名前 | 内容 |
|---|---|
| Capacitated VRP; CVRP | 車両に載せることができる荷物の容量の制約付き |
| VRP with Time Windows; VRPTW | 何時から何時の間に集荷or配達して欲しいという顧客の希望の時間帯の制約付き |
| Distance Constrained VRP; DCVRP | 車両が走行できる距離の制約付き |
| Multi Depots VRP; MDVRP | 車両が出発・到着する車両倉庫(depot)が複数ある場合のVRP |
| VRP with Pick-up and Delivery; VRPPD | 集荷および配達を行う場合のVRP。荷物の集荷が配達より先という制約が付く |
この辺りをサーベイしているような資料とか探せばある気はしますけど、本題じゃないので、今回は基本的な車両に積載キャパシティがある場合によるVRP(上記でいうCVRP)を、PuLPを使って解いてみます。
先ほどと同様に、各拠点の座標と、その場所から運んでもらいたい需要 demand を適当に作成します。
1台あたりの車両の積載キャパシティは 8 と設定しました。
# define VRP
n_customer = 9
n_point = n_customer + 1
vehicle_capacity = 8
df = pd.DataFrame({
'x': np.random.randint(0, 100, n_point),
'y': np.random.randint(0, 100, n_point),
'demand': np.random.randint(1, 5, n_point),
})
df.iloc[0]['x'] = 0
df.iloc[0]['y'] = 0
df.iloc[0]['demand'] = 0
df
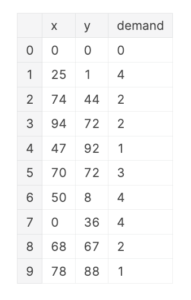
様子を確認してみるとこんな感じ。
各拠点の場所と括弧で需要を描きました。
# check VRP state
plt.figure(figsize=(5, 5))
# draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
demand = row['demand']
plt.text(row['x'] + 1, row['y'] + 1, f'{i}({demand})')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id(demand)')
plt.show()
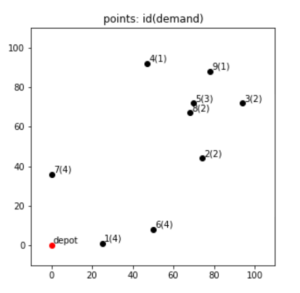
これを、積載キャパシティが 8 の車両を使って、総移動距離を最小化した時に必要な台数およびそれぞれの運搬経路を求めるコードが以下の通りです。
demands = df['demand'].values
# set problem
problem = pulp.LpProblem('cvrp_mip', pulp.LpMinimize)
# set variables
x = pulp.LpVariable.dicts('x', ((i, j) for i in range(n_point) for j in range(n_point)), lowBound=0, upBound=1, cat='Binary')
n_vehicle = pulp.LpVariable('n_vehicle', lowBound=0, upBound=100, cat='Integer')
# set objective function
problem += pulp.lpSum([distances[i][j] * x[i, j] for i in range(n_point) for j in range(n_point)])
# set constrains
for i in range(n_point):
problem += x[i, i] == 0
for i in range(1, n_point):
problem += pulp.lpSum(x[j, i] for j in range(n_point)) == 1
problem += pulp.lpSum(x[i, j] for j in range(n_point)) == 1
problem += pulp.lpSum(x[i, 0] for i in range(n_point)) == n_vehicle
problem += pulp.lpSum(x[0, i] for i in range(n_point)) == n_vehicle
# eliminate subtour
subtours = []
for length in range(2, n_point):
subtours += itertools.combinations(range(1, n_point), length)
for st in subtours:
demand = np.sum([demands[s] for s in st])
arcs = [x[i, j] for i, j in itertools.permutations(st, 2)]
problem += pulp.lpSum(arcs) <= np.max([0, len(st) - np.ceil(demand / vehicle_capacity)])
# solve problem
status = problem.solve()
# output status, value of objective function
status, pulp.LpStatus[status], pulp.value(problem.objective)
"""
(1, 'Optimal', 598.2419050203686)
"""
やっぱり巡回セールスマン問題の時と定式化が結構似てきますが、特に、
problem += pulp.lpSum(x[i, 0] for i in range(n_point)) == n_vehicle
problem += pulp.lpSum(x[0, i] for i in range(n_point)) == n_vehicle
の部分で、使っている車両の台数の辻褄を合わせていて(出て行く車両と帰ってくる車両の数を合わせる)、かつ、
for st in subtours:
demand = np.sum([demands[s] for s in st])
arcs = [x[i, j] for i, j in itertools.permutations(st, 2)]
problem += pulp.lpSum(arcs) <= np.max([0, len(st) - np.ceil(demand / vehicle_capacity)])
で需要と車両のキャパシティ制限の制約を制御しています。
上記で解析すると、総移動距離は 598.24 となり、
pulp.value(n_vehicle)
"""
3.0
"""
使う車両の台数は3台となりました。
最適化された結果を可視化してみると、以下のような感じです。
# check TSP problem and optimized route
plt.figure(figsize=(5, 5))
# draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
demand = row['demand']
plt.text(row['x'] + 1, row['y'] + 1, f'{i}({demand})')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id(demand)')
# draw optimal route
cmap = matplotlib.cm.get_cmap('Dark2')
routes = [(i, j) for i in range(n_point) for j in range(n_point) if pulp.value(x[i, j]) == 1]
for v in range(int(pulp.value(n_vehicle))):
# identify the route of each vehicle
vehicle_route = [routes[v]]
while vehicle_route[-1][1] != 0:
for p in routes:
if p[0] == vehicle_route[-1][1]:
vehicle_route.append(p)
break
# draw for each vehicle
arrowprops = dict(arrowstyle='->', connectionstyle='arc3', edgecolor=cmap(v))
for i, j in vehicle_route:
plt.annotate('', xy=[df.iloc[j]['x'], df.iloc[j]['y']], xytext=[df.iloc[i]['x'], df.iloc[i]['y']], arrowprops=arrowprops)
plt.show()
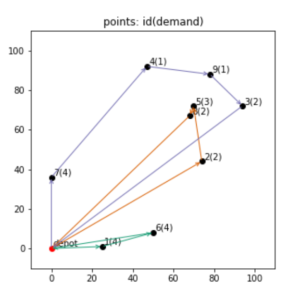
それぞれの色が車両を表して、3台を使って、上記のように回ってもらう経路が総移動距離最小化の最適解となっています。
割と各車両の走行距離に差がある結果になっていますね。
何かしらの、それぞれの車両の移動距離(業務時間)に制約を入れたりするとか、車両を利用することにかかる時間や距離当たりのコストで目的関数を構築するなどの工夫をした方が良いかもしれません。
まとめ
TSP、VRPの簡単な問題設定において、PuLPで最適解を求めるコードを公開しました。
今回は特に多くの制約は設けてはおらず、かつ問題の規模(都市の数)はとても少ないもので解いていますので、瞬間的に最適解は求められますが、これを色々と増やしていくと、組合せ爆発的に解析時間もかかるようになっていきます。
最近、数理最適化も勉強をしているのですが、機械学習・ディープラーニングとも異なるし、統計学・ベイズ統計などとも異なる感じで、難しいですね。
特に、シミュレーションとかエージェントとかみたいに、プログラムで最適化したい対象を模倣して動かしてみるような感じではない場合が多く、定式化でどんどん行動の辻褄を合わせていくような感覚に近いので、この辺りが直感的な思考通りに作っていけなさみたいなものがあります。
数理最適化問題の経験歴が長いわけではないので、感想みたいなものですけども。
個人的には、どちらかというと、強化学習みたいなエージェントを模写して行動させて学習させる方法論の方がしっくりくるかもです。


コメント