スポンサーリンク

Pythonで地理データを階層ベイズモデルで推定・可視化してみた

PyMC Python データビジュアライゼーション データ分析 ベイジアンモデル 地理データ
e-Stat APIをPythonから使って地理データを可視化してみた
e-Statは日本政府が調査した統計データを閲覧・ダウンロードできるよう管理されたポータルサイトです。 このサイトからよく人口データなどをダウンロードして利用しており、以前からお世話になっているのですが、実はAPI機能も提供しているようで、前々から少し気になっておりましたので、この度、PythonからAPI経由でデータ取得をして、可視化するところまでをやってみました。
ie110704.net
2016-11-11

続き。

まぁ、続きと言いますか、少し前に書籍の『岩波データサイエンスVol.4 -地理空間情報処理-』を読みました。

そういえば、今は『Vol.5 -スパースモデリングと多変量データ解析-』も出ていますね。

岩波データサイエンス Vol.4
岩波データサイエンス刊行委員会 | 販売者: 株式会社 岩波書店 | 2017/10/19
岩波データサイエンス Vol.5
岩波データサイエンス刊行委員会 | 販売者: 株式会社 岩波書店 | 2017/10/19

で、Vol4の中で、e-Statから取得した地理データから階層ベイズモデルを用いて地域特徴を推定する事例を紹介されており、面白そうなのでやってみました。

ただ、上記書籍では、e-Statから普通にダウンロードしたデータを、Stan/BUGSなどのベイズ統計言語でデータを推定し、そこからまた別の地理データ可視化ソフトウェアを使って、推定結果を可視化していましたので、今回はそれらを全てPythonで一括してやってみようと思います。

問題と統計モデル

地域別の自殺リスクを推定する

上記の書籍では、地図上に表現された地理的な隣接情報を利用して、空間的な相関を考慮した階層ベイズモデルを用いた「地域別の自殺リスク」の推定を行って、その結果をコロプレスマップとして地図上に可視化、ということをやっています。

e-Statでダウンロードした地域別の自殺数を用いて、普通に自殺リスクを算出しようとすると、地域によっては値が小さすぎて、適切な自殺リスクが得られないため、ベイズモデルで空間的な相関を導入することで、これを解決するという方法を提案されています。

標準化死亡比（SMR）

「自殺リスク」とは何かという話ですが、これについては疫学の分野において、ある基準集団と比べて相対的にリスクが高いか低いかを表す指標で、標準化死亡比（SMR）というものがあります。

まず、ある地区が、基準集団と同じリスクを持つ場合の死亡数を、期待死亡数と呼び、下記で計算できます。

    \[y = \Sigma_i(\frac{Z_i}{N_i}{\times}{n_i})\]

Z_i : 基準集団での年齢iの死亡数
N_i : 基準集団の年齢iの人口
n_i : その地域の年齢iの人口

観測された死亡数が、この期待死亡数に比べて多い場合、死亡のリスクが大きいと考えられ、これを標準化死亡比（SMR）と言います。

    \[SMR=\frac{z}{y}\]

z : 観測死亡数

データからこの比率を単純に計算することもできますが、今回はこれを推定する方向で実装してみます。

統計モデル

上記を踏まえて、SMRを地域の相関が考慮されるように推定する階層ベイズモデルを次のように設計します。

    \[z_i{\sim}Poisson(\lambda_i)\]

    \[\lambda_i=y_i\exp(\phi_i+\psi_i)\]

    \[\phi_i{\sim}N(0, \sigma^2)\]

    \[\psi_i|\psi_{j{\neq}i}{\sim}N(\frac{1}{m_i}\Sigma_{j{\in}n(i)}\psi_i, \frac{1}{m_i}\sigma^2_{\psi})\]

z_i：地区iの死亡数
y_i：地区iの期待死亡数
\phi_i：地区i固有の効果を表すパラメータ
\psi_i：地区iは隣接地区と似通った傾向を持つことを表すパラメータ

データは死亡数なのでポアソン-対数正規モデルとし、ポアソン分布のパラメータに地域相関のあるSMRがかかる形にしています。

ここで、\exp(\phi_i+\psi_i)が地区iのSMRの推定値に相当します。

PyMC

PyMCは、ベイズ統計モデルの設定とMCMCサンプリングをPythonで実行できるライブラリです。

PyMC3 : https://github.com/pymc-devs/pymc3

PyMCにはPyMC2系列とPyMC3系列があるようです。

どっちがどうとかはよく分かりませんが、PyMC3の方が早いとかどこかで見ましたので、こちらを使うことにしました。

ちなみにPythonでのベイズ統計ライブラリといえば、Stanを実行できるPyStanもあります。

こちらでもよかったのですが、モデルの記述がまんまStanになりますので、ちょっと新鮮味を求めて今回はPyMCを使ってみました笑

比較してみると結構記述はPyMCの方がスマートで、直感的にモデルの構造が分かりやすい記述なのかなと思います。

ただ、インターネット上に情報がなく、PyStanは結局Stanですので、StanやRStanで書かれた情報とかも参考になる分、こちらは実装に苦労しました...。

PyMCの実装例

import numpy as np
import pymc3 as pm
%matplotlib inline
import matplotlib.pylab as plt

N = 10
x_samples, y_samples = [], []
for i in range(N):
    x = round(np.random.rand()*4+3, 1) # 3.0〜7.0までの乱数
    mu = np.exp(1.5+0.1*x) # ポアソン分布の平均
    y = np.random.poisson(mu)
    x_samples.append(x)
    y_samples.append(y)

with pm.Model() as model:
    beta1 = pm.Normal("beta1", mu=0, tau=1000)
    beta2 = pm.Normal("beta2", mu=0, tau=1000)
    mu = np.exp(beta1+beta2*x_samples)
    y = pm.Poisson("y", mu=mu, observed=y_samples)
    start = pm.find_MAP()
    step = pm.NUTS()
    trace = pm.sample(1000, step, start)
    pm.traceplot(trace)

PyStanの実装例

import numpy as np
import pystan
%matplotlib inline
import matplotlib.pylab as plt

N = 10
x_samples, y_samples = [], []
for i in range(N):
    x = round(np.random.rand()*4+3, 1) # 3.0〜7.0までの乱数
    mu = np.exp(1.5+0.1*x) # ポアソン分布の平均
    y = np.random.poisson(mu)
    x_samples.append(x)
    y_samples.append(y)

stan_data = {'N': N, 'x': x_samples, 'y': y_samples}

model = """
data {
    intN;
    vector[N] x;
    int y[N];
}
parameters {
    real beta1;
    real beta2;
}
model {
    for (i in 1:N){
        y[i] ~ poisson(exp(beta1+beta2*x[i]));
    }
    beta1 ~ normal(0, 1000);
    beta2 ~ normal(0, 1000);
}
"""

fit = pystan.stan(model_code=model, data=stan_data, iter=1000, chains=1)
fit.plot()
plt.show()

地理データを階層ベイズモデルで推定・可視化

それでは、実装になります。

前回投稿同様に、データはe-Stat APIから直接取得します。

e-Stat API : http://www.e-stat.go.jp/api/

推定はPyMC3で行い、可視化は前回同様、Foliumを使って、そのまま分析環境で可視化してみます。

Folium : https://github.com/python-visualization/folium

コードが下記になります。

import re
import csv
import numpy as np
import pandas as pd
import urllib.request
import folium
from IPython.display import display
import pymc3 as pm
%matplotlib inline
import matplotlib.pylab as plt

appid = "appid"
api_version = "2.1"
base_url = "http://api.e-stat.go.jp/rest/{api_version}/app/".format(api_version=api_version)
get_type = "getStatsList"
#stats_code = "00450011" # 人口動態調査
#stats_code = "00200524" # 人口推計
#stats_code = "00200521" # 国勢調査
#print(base_url + "{}?appId={}&statsCode={}".format(get_type, appid, stats_code))

# 都道府県別の自殺数
get_type="getStatsData"
stats_data_id="0003030127"
url =base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)

get_type="getSimpleStatsData"
stats_data_id="0003030127"
lv_cat_01="2"
cd_cat_02="129"
cd_cat_03="1"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&lvCat01={}&cdCat02={}&cdCat03={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, lv_cat_01, cd_cat_02, cd_cat_03, section_header_flg)
data_pref_die = urllib.request.urlopen(url).read().decode("utf8")

# 都道府県別、年齢階級別の人口
get_type="getStatsData"
stats_data_id="0003014716"
url = base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)

get_type="getSimpleStatsData"
stats_data_id="0003014716"
cd_cat_01="000"
cd_cat_02_from="01001"
cd_cat_02_to="04018"
lv_area="2"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&cdCat01={}&cdCat02From={}&cdCat02To={}&lvArea={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, cd_cat_01, cd_cat_02_from, cd_cat_02_to, lv_area, section_header_flg)
data_pref_age_pop = urllib.request.urlopen(url).read().decode("utf8")

# 全国、年齢階級別の自殺数
get_type="getStatsData"
stats_data_id="0003031497"
url =base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)

get_type="getSimpleStatsData"
stats_data_id="0003031497"
lv_cat_01="2"
cd_cat_02="268"
cd_cat_03="1"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&lvCat01={}&cdCat02={}&cdCat03={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, lv_cat_01, cd_cat_02, cd_cat_03, section_header_flg)
data_all_age_die = urllib.request.urlopen(url).read().decode("utf8")

# 全国、年齢階級別の人口
get_type="getStatsData"
stats_data_id="0003014709"
url = base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)

get_type="getSimpleStatsData"
stats_data_id="0003014709"
cd_cat_01 = "000"
cd_cat_02 = "001"
cd_cat_03_from = "01001"
cd_cat_03_to = "01021"
cd_time = "2009000000"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&cdCat01={}&cdCat02={}&cdCat03From={}&cdCat03To={}&cdTime={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, cd_cat_01, cd_cat_02, cd_cat_03_from, cd_cat_03_to, cd_time, section_header_flg)
data_all_age_pop = urllib.request.urlopen(url).read().decode("utf8")

# 都道府県別の自殺数、データフレーム化
dlines = data_pref_die.splitlines()[2:]
jiscode, cnt = [], []
for line in dlines:
    line2 = line.replace('"', "").split(",")

    jiscode_tmp = line2[2]
    jiscode_tmp = int(jiscode_tmp)-1
    if jiscode_tmp > 47:
        continue
    jiscode_tmp = "0" + str(jiscode_tmp) if jiscode_tmp < 10 else str(jiscode_tmp)
    jiscode.append(jiscode_tmp)

    cnt_tmp = int(line2[11])
    cnt.append(cnt_tmp)

df_pref_die = pd.DataFrame({"jiscode": jiscode, "cnt": cnt})

# 都道府県コードマスタ、都道府県別、年齢階級別の人口、データフレーム化
dlines = data_pref_age_pop.splitlines()[2:]
jiscode, name, age_cls, cnt = [], [], [], []
for line in dlines:
    line2 = line.replace('"', "").split(",")

    jiscode_tmp = line2[6]
    jiscode_tmp = jiscode_tmp.replace("000", "")
    jiscode.append(jiscode_tmp)

    name_tmp = line2[7]
    name.append(name_tmp)

    age_cls_tmp = line2[5]
    age_cls_tmp = age_cls_tmp.replace("歳", "").split("～")
    age_cls_tmp = "85_" if len(age_cls_tmp) == 1 else age_cls_tmp[0]+"_"+age_cls_tmp[1]
    age_cls.append(age_cls_tmp)

    cnt_tmp = line2[11]
    cnt_tmp = int(cnt_tmp)*1000
    cnt.append(cnt_tmp)

df_pref_age_pop = pd.DataFrame({"jiscode": jiscode, "age_cls": age_cls, "cnt": cnt})
df_pref_age_pop_14 = df_pref_age_pop.query("age_cls=='0_4' | age_cls=='5_9' | age_cls=='10_14'")
df_pref_age_pop_14 = df_pref_age_pop_14[["jiscode", "cnt"]].groupby("jiscode").sum().reset_index()
col14 = pd.DataFrame([["_14"]*47]).T
col14.columns = ["age_cls"]
df_pref_age_pop_14 = pd.concat([df_pref_age_pop_14, col14], axis=1)
df_pref_age_pop = df_pref_age_pop.query("age_cls!='0_4' & age_cls!='5_9' & age_cls!='10_14'")
df_pref_age_pop = pd.concat([df_pref_age_pop, df_pref_age_pop_14], axis=0)
jiscode = sorted(set(jiscode), key=jiscode.index)
name = sorted(set(name), key=name.index)
df_pref_mst = pd.DataFrame({"jiscode": jiscode, "name": name})

# 全国の年齢階級別の自殺数、データフレーム化
dlines = data_all_age_die.splitlines()[2:]
age_cls, cnt = [], []
for line in dlines:
    line2 = line.replace('"', "").split(",")

    age_cls_tmp = line2[3]
    if age_cls_tmp == "不詳":
        continue
    age_cls_tmp = re.sub(r"歳|～", "", age_cls_tmp)
    age_cls_tmp = "100_" if age_cls_tmp == "100" else str(int(age_cls_tmp.split("-")[0]))+"_"+str(int(age_cls_tmp.split("-")[-1]))
    age_cls.append(age_cls_tmp)

    cnt_tmp = line2[-1]
    cnt_tmp = 0 if cnt_tmp == "-" else int(cnt_tmp)
    cnt.append(cnt_tmp)

age_cls = age_cls[3:-3]
age_cls.insert(0, "_14")
age_cls[-1] = "85_"
cnt_15 = np.sum(cnt[0:3])
cnt_85 = np.sum(cnt[-4:])
cnt = cnt[3:-4]
cnt.insert(0, cnt_15)
cnt.append(cnt_85)
df_all_age_die = pd.DataFrame({"age_cls" : age_cls, "cnt" : cnt})

# 全国の年齢階級別の人口、データフレーム化
dlines = data_all_age_pop.splitlines()[2:]
age_cls, cnt = [], []
for line in dlines:
    line2 = line.replace('"', "").split(",")

    age_cls_tmp = line2[5]
    age_cls_tmp = re.sub(r"歳", "", age_cls_tmp).split("～")
    age_cls_tmp = "100_" if len(age_cls_tmp) == 1 else age_cls_tmp[0]+"_"+age_cls_tmp[1]
    age_cls.append(age_cls_tmp)

    cnt.append(int(line2[-1])*1000)

age_cls = age_cls[3:-3]
age_cls.insert(0, "_14")
age_cls[-1] = "85_"
cnt_15 = np.sum(cnt[0:3])
cnt_85 = np.sum(cnt[-4:])
cnt = cnt[3:-4]
cnt.insert(0, cnt_15)
cnt.append(cnt_85)
df_all_age_pop = pd.DataFrame({"age_cls" : age_cls, "cnt" : cnt})

# 都道府県別、期待死亡数、データフレーム
df_y_tmp = pd.merge(df_all_age_pop, df_all_age_die, how="inner", on="age_cls", suffixes=("_pop", "_die"))
df_y_tmp = df_y_tmp.assign(y_tmp=df_y_tmp["cnt_die"]/df_y_tmp["cnt_pop"])
df_y_tmp = df_y_tmp.drop("cnt_pop", axis=1).drop("cnt_die", axis=1)
df_y_tmp = pd.merge(df_pref_age_pop, df_y_tmp, how="inner", on="age_cls")
df_y_tmp = df_y_tmp.assign(y=df_y_tmp["y_tmp"]*df_y_tmp["cnt"])
df_y_tmp = df_y_tmp.drop("cnt", axis=1).drop("y_tmp", axis=1)
df_y = df_y_tmp[["jiscode", "y"]].groupby("jiscode").sum().reset_index()

# 都道府県別、隣接都道府県、データフレーム
from_names, to_names = [], []
with open("japan_adj.csv", "r") as f:
    reader = csv.reader(f)

    for row in reader:
        from_name_tmp = row[1].replace("\xa0", "").replace(" ", "")
        to_names_tmp = row[4].replace("\xa0", "").replace(" ", "").split(",")

        for to_name_tmp in to_names_tmp:
            from_names.append(from_name_tmp)
            to_names.append(to_name_tmp)

from_names = from_names[0:-1]
to_names = to_names[0:-1]
df_adj_tmp = pd.DataFrame({"f_name": from_names, "t_name": to_names})
df_adj_tmp = pd.merge(df_adj_tmp, df_pref_mst, how="left", left_on="f_name", right_on="name").drop("name", axis=1).rename(columns={"jiscode": "f_jiscode"})
df_adj_tmp = pd.merge(df_adj_tmp, df_pref_mst, how="left", left_on="t_name", right_on="name").drop("name", axis=1).rename(columns={"jiscode": "t_jiscode"})
df_adj = df_adj_tmp.drop("f_name", axis=1).drop("t_name", axis=1)

# 自殺数、期待死亡数、隣接行列 for 階層ベイズモデル
jiscodes = list(df_pref_mst["jiscode"].values.flatten())
n = len(jiscodes)
y_samples, z_samples, adj_matrix, d_matrix = [], [], [], []
for i in range(0, n):
    y = df_y[df_y["jiscode"] == jiscodes[i]]["y"].values[0] # 期待死亡数
    y_samples.append(y)

    z = df_pref_die[df_pref_die["jiscode"] == jiscodes[i]]["cnt"].values[0] # 自殺数
    z_samples.append(z)

    adjs = df_adj[df_adj["f_jiscode"] == jiscodes[i]]["t_jiscode"].values #  隣接JISCODE
    adjs_idx = np.zeros(n)
    for j in adjs:
        adjs_idx[jiscodes.index(j)] = 1
    adj_matrix.append(adjs_idx)

    d_idx = np.zeros(n)
    d_idx[i] = 2
    d_matrix.append(d_idx)

jiscodes = np.array(jiscodes, dtype=object) # JISCODE
y_samples = np.array(y_samples, dtype=int) # 期待死亡数
z_samples = np.array(z_samples, dtype=int) # 自殺数
adj_matrix = np.array(adj_matrix, dtype=int).reshape(n, n) # 隣接行列
d_matrix = np.array(d_matrix, dtype=int).reshape(n, n) # 自身の行列

# ベイズモデルで推定
with pm.Model() as model:
    p1 = pm.Uniform("p1", lower=0, upper=1)
    p2 = pm.Uniform("p2", lower=0, upper=1)
    tau_phi = pm.Gamma("tau_phi", alpha=0.5, beta=0.005)
    phi = pm.Normal("phi", mu=0, tau=tau_phi)
    t = p1*d_matrix+p2*adj_matrix
    psi = pm.MvNormal('psi', mu=0, cov=t, shape=n)
    lamb = np.exp(np.log(y_samples)+phi+psi)
    z = pm.Poisson("z", mu=lamb, observed=z_samples)

    start = pm.find_MAP()
    step = pm.NUTS()
    trace = pm.sample(1000, step, start)
    #pm.traceplot(trace)
    #pm.summary(trace)

phi_m = np.mean(trace["phi"])

psi_m = []
t = trace["psi"].transpose()
for i in t:
    psi_m.append(np.mean(i))

smr_est = np.exp(phi_m+psi_m)

# 都道府県別、推定SMR
df_smr_est = pd.DataFrame({"jiscode" : jiscodes, "smr_est" : smr_est})
display(df_smr_est)

# コロプレスマップに推定値を可視化
location = [35.709634, 139.392101]
tiles="Stamen Toner"
zoom_start = 10
map = folium.Map(location=location, tiles=tiles, zoom_start=zoom_start)
map.choropleth(
    geo_path="japan.geojson",
    data=df_smr_est,
    columns=["jiscode", "smr_est"],
    key_on="properties.JCODE",
    threshold_scale=[0.90, 0.95, 1.00, 1.05, 1.10, 1.15],
    fill_color="YlGnBu",
    fill_opacity=0.7,
    line_opacity=0.3,
    reset=True)
display(map)

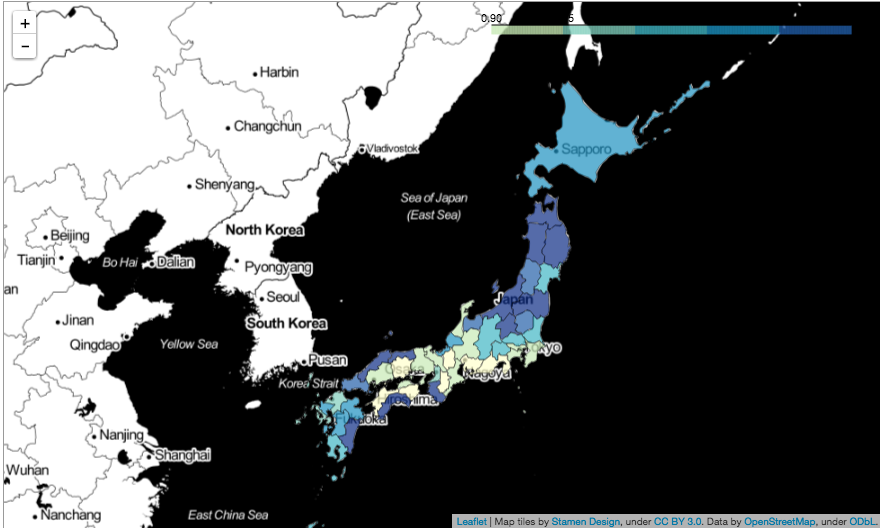
都道府県別でリスク推定をしてみた結果になります。

思ったよりも、地方の方がリスクが高いように推定されているみたいで、期待死亡数の方も、全体的に地方の方が高い傾向にありました。

ちなみに、書籍では市区町村別のデータにしていたため、おそらく欠損とかもある中、うまく推定をしているのでしょうが、そのデータがなぜか見つかりませんでした...。

本当は同じデータを使って、答え合わせしたかったのですが...。

それでも、実装の勉強になりました。

個人的には、地域相関を入れるCAR事前モデルの部分が、Stanですとパッケージで自動的にやってくれるみたいですが、PyMCはそれがないので自前で作らなければならず、そこが正しく出来ているのか不安です。

特に、多変量ガウス分布の分散共分散行列で地域相関を表現させる際の重みの調整はどうすれば良いか分からず、結局そこにも事前分布を入れて、回してみるようにしてみた、といったところです。

スポンサーリンク

コメント