タイトルの通り、為替データを畳み込みニューラルネットワーク(CNN)で読み込んで予測させるまでを、Chainerで実装してみました。
今回は順を追って、データの取得と加工、モデルの構築、学習と予測をしていきます。
まずは為替のデータの取得です。
Pythonのライブラリ pandas_datareader を使って、日付ごとのドル円価格のデータを取得しました。
期限は適当に区切って、7年分を取得してきています。
import numpy as np
import pandas as pd
from pandas_datareader import data, wb
start = "2010-08-01"
end = "2017-08-01"
usdjpy = data.DataReader("DEXJPUS", "fred", start, end) # ドル円レート from セントルイス連邦準備銀行
display(usdjpy.head())

いったん様子を確認するため、プロットしてみます。
import matplotlib
import matplotlib.pylab as plt
matplotlib.style.use("ggplot")
# 原系列プロット
usdjpy_tmp = usdjpy.dropna()
usdjpy_tmp.plot(color="cyan", figsize=(15,7))
plt.show()
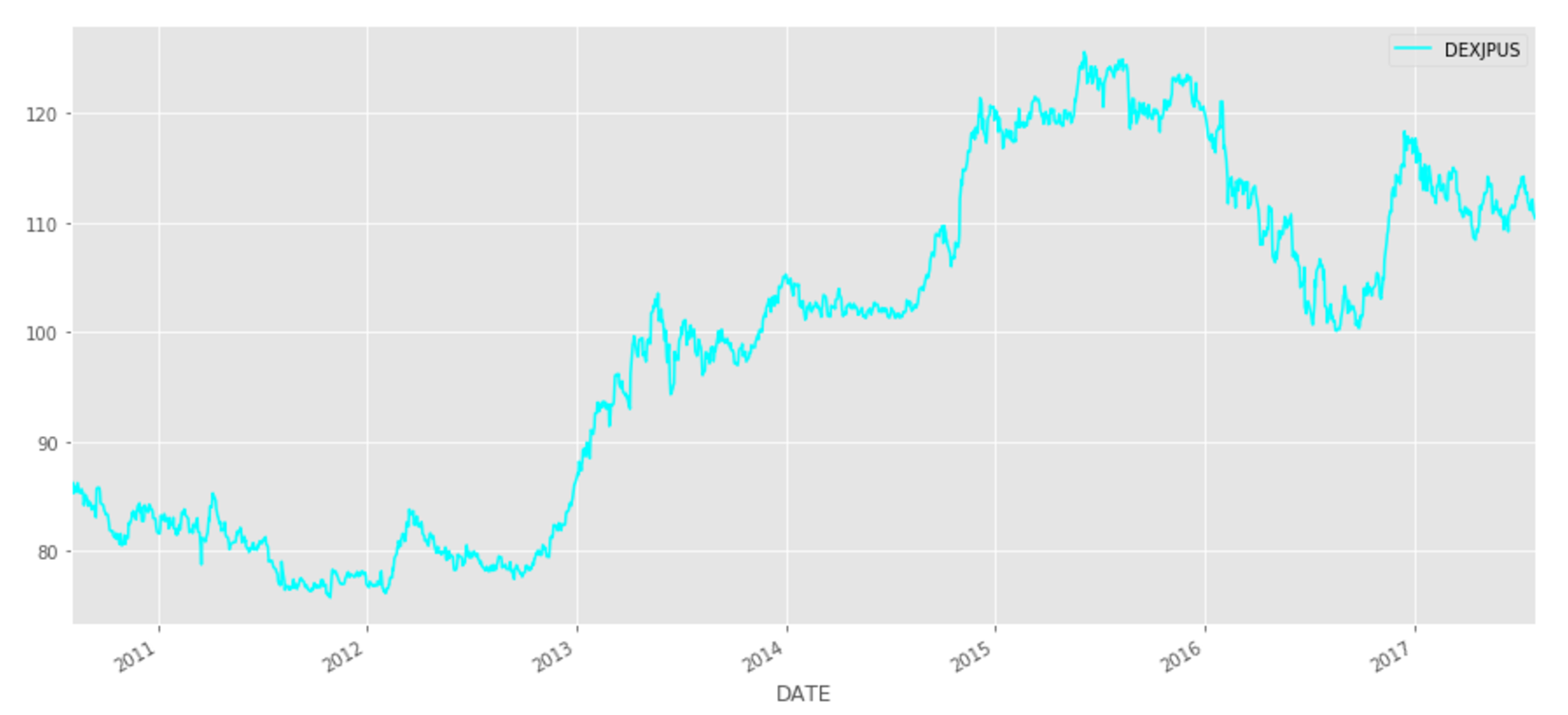
さて、この時系列のデータから、ある程度、値の動きを読み込ませた後にその次の値は上がるか・下がるかの予測をできるかどうか、モデルを構築して試してみます。
方法としては、ある程度の時系列の長さを決め、その間の値の上がり具合・下がり具合を数値化したものをCNNで読み込んで、次は「上がる」か「下がる」の分類モデルを構築することにします。
まずは原系列から差分系列に変換し、上下の具合を数値化するため、[0,1]区間に正規化します。
from sklearn.preprocessing import MinMaxScaler
# データ加工
scaler = MinMaxScaler(feature_range=(0,1))
usdjpy_tmp = usdjpy.dropna()
usdjpy_tmp = usdjpy_tmp.diff().dropna() # 差分(変動)の系列にする
usdjpy_tmp = np.array(usdjpy_tmp["DEXJPUS"].values).reshape(-1,1) # numpy配列にする
usdjpy_tmp = scaler.fit_transform(usdjpy_tmp) # 正規化
plt.figure(figsize=(15,7))
plt.plot(usdjpy_tmp, color="cyan")
plt.show()
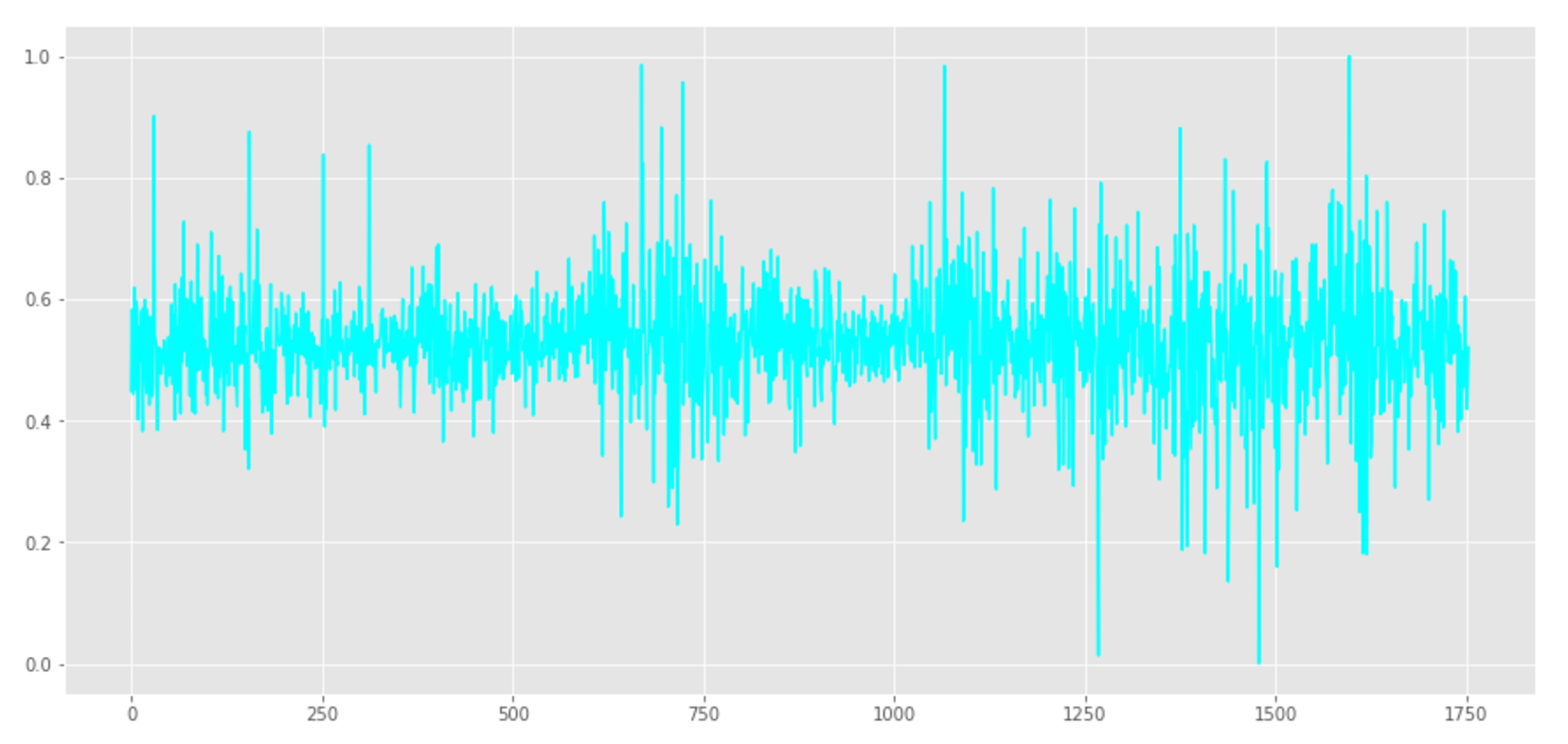
次に、CNNで読み込める教師データの形にします。
系列データから決めた時系列の長さ分だけ取得してきて、入力を上下の具合を1次元の画像と見立てたもの、出力を1(上がる)か0(下がる)に変換していきます。
SEQ_SIZE = 50
dataset = []
for i in range(len(usdjpy_tmp)-SEQ_SIZE): # SEQ_SIZE分の系列をとり、その次の値が上がっているか下がっているかのラベルにする
x = usdjpy_tmp[i:i+SEQ_SIZE]
t_tmp = usdjpy_tmp[i+SEQ_SIZE]
t = 1 # 上がっている
if x[-1] > t_tmp: # 下がっている
t = 0
x = np.array(x, dtype="float32").reshape(1, 1,SEQ_SIZE) # 畳み込みニューラルネットワークにするので、時系列は1次元の画像と見立てる (in_channel, height_size, width_size)
t = np.array(t, dtype="int32")
dataset.append((x,t))
N = len(dataset)
print("教師データ件数: ", N)
# 一部確認してみる
for i in range(5):
print(dataset[i][0][0])
plt.figure(figsize=(30,140))
plt.imshow(dataset[i][0][0], cmap="gray")
plt.show()

一部データを確認してみたものが上記となります。
上記のように、値がどう動いてきたかを色の濃淡の画像で表す感じになります。
途中とても白い部分がありますが、ここが原系列の中でもかなり大きく値が変動した部分となっているようです。
実際の値を確認してみると、0.90144926がその箇所のようです。
これを分類するCNNをChainerで組んでいきます。
入力する画像(時系列)は縦方向の次元が1次元となっていますので、フィルターの縦サイズは1とし、横サイズは適当に決めることにします。
出力層の次元数は、1(上がる)か0(下がる)なので2です。
import chainer
from chainer import Chain, optimizers, training
from chainer.training import extensions
import chainer.functions as F
import chainer.links as L
# CNNクラスの定義
class CNN(Chain):
def __init__(self):
# クラスの初期化
super(CNN, self).__init__(
conv1 = L.Convolution2D(1, 20, (1,5)),
conv2 = L.Convolution2D(20, 50, (1,5)),
l1 = L.Linear(500, 100),
l2 = L.Linear(100, 100),
l3 = L.Linear(100, 2)
)
def __call__(self, x):
# 順伝播の計算を行う関数
# :param x: 入力値
h = F.max_pooling_2d(F.relu(self.conv1(x)), 2)
h = F.max_pooling_2d(F.relu(self.conv2(h)), 2)
h = F.relu(self.l1(h))
h = F.relu(self.l2(h))
y = self.l3(h)
return y
上記のように、畳み込み層2層+全結合3層のモデルを用意しました。
これに先ほど作成した教師データから、学習用、テスト用に分割し、学習と予測精度の評価をしてみます。
学習の実装が下記になります。
EPOCH_NUM = 30
BATCH_SIZE = 200
# モデルの定義
model = L.Classifier(CNN())
optimizer = optimizers.Adam()
optimizer.setup(model)
# 学習開始
print("Train")
train, test = chainer.datasets.split_dataset_random(dataset, N-100)
train_iter = chainer.iterators.SerialIterator(train, BATCH_SIZE)
test_iter = chainer.iterators.SerialIterator(test, BATCH_SIZE, repeat=False, shuffle=False)
updater = training.StandardUpdater(train_iter, optimizer, device=-1)
trainer = training.Trainer(updater, (EPOCH_NUM, "epoch"), out="result")
trainer.extend(extensions.Evaluator(test_iter, model, device=-1))
trainer.extend(extensions.LogReport())
trainer.extend(extensions.PrintReport( ["epoch", "main/loss", "validation/main/loss", "main/accuracy", "validation/main/accuracy", "elapsed_time"])) # エポック、学習損失、テスト損失、学習正解率、テスト正解率、経過時間
#trainer.extend(extensions.ProgressBar()) # プログレスバー出力
trainer.run()
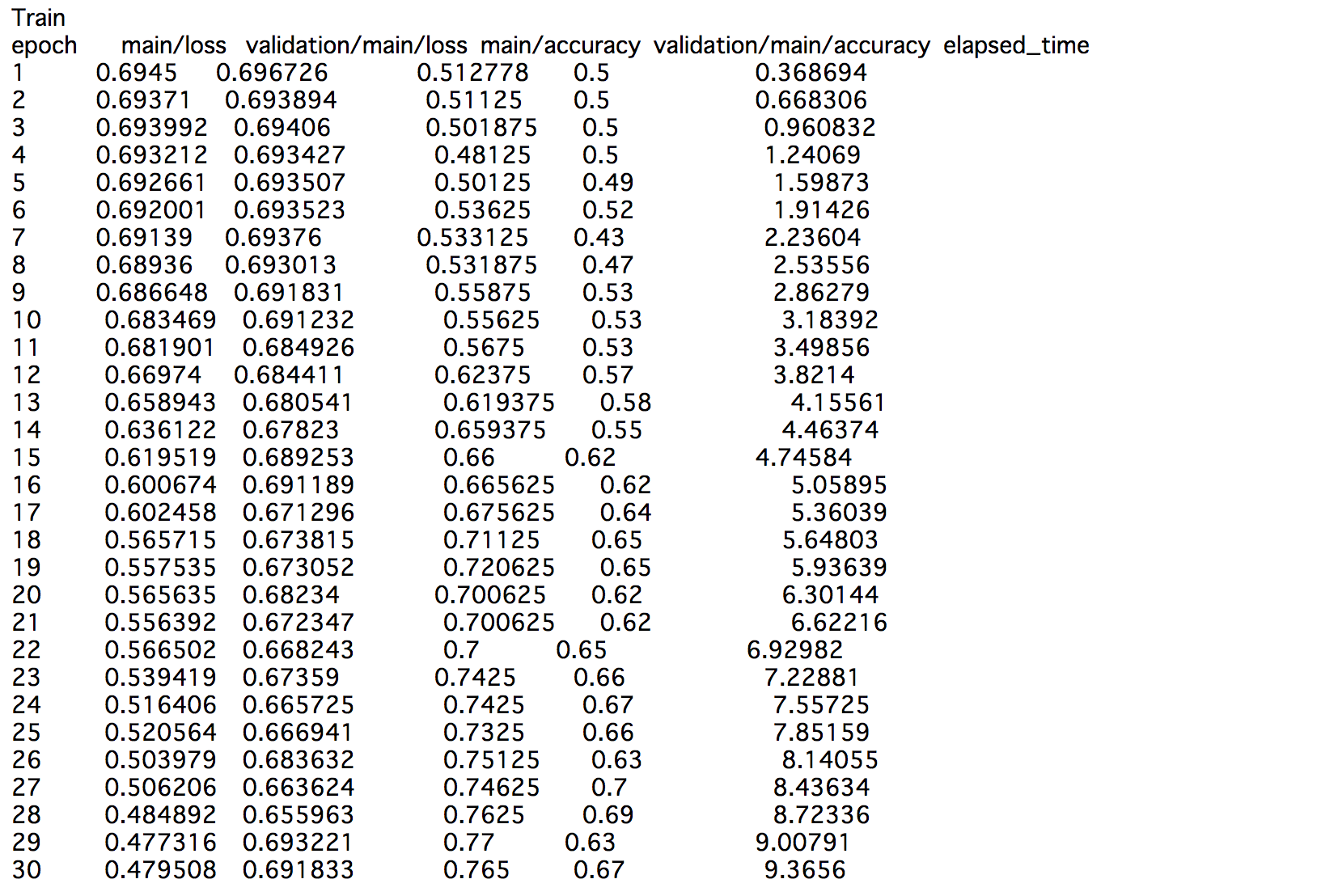
テストデータに対して、7割近くまで当てられるようになりました。
個人的には、思っていた以上に当たっていて、びっくりしています笑
こうしてニューラルネットワークである程度予測できるということは、やはり何かしら規則的なものがあるのでしょうか。
素人からすると次が上がるか下がるかなんて全く予測できませんが、経験多く積んだ投資家や専門家から見ると、少なくともこの程度の精度以上には当てられるのかもしれません。
株価の世界などで俗に言われるテクニカル分析というものが、レートの形から将来の値動きを予測する手法と言われていますので、何かしら予測する方法があるのだろうと思います。
ところで、今回はCNNを使いましたが、こういった時系列データはむしろ再帰的ニューラルネットワーク(RNN)の方が合っているのではないかと思いますが、実はRNNでも試しており、同程度の予測率が出せることが確認できています。
ただしRNNですと、やはり計算量が大きくなりがちですので、より早いモデルとしてCNNを使った場合はどうなるのかの検証のため、今回はCNNを試してみたといったところです。
フィルターで読み取った上でマックスプーリングして、ある程度、事前の系列を集約してしまった上でも、先ほどのような規則的なものが現れると考えても良さそうです。
追記(2017-12-16)
記事を作成した時は「何か間違いがあるだろうなー」とは思っていましたが、やはり正しくないことをしていたようです。
下記の突っ込みコメントをいただきました。
テスト用データを作る際に、ランダムに分離していますが、
元のデータは時系列データにウィンドウをスライドしながら作ったものなので、
テスト用データの中に、「学習データと1つずれただけ」のような、学習データと
部分的に被るデータが多数含まれる事になります。
そのため、元のデータにMomentumが存在するとき、結果が不正確に高く評価されると思います。
なるほど涙
データをスライドしながら作成するまではともかく、学習と評価にそれを混ぜてしまっていました。
そうなると、部分的に全く一緒のデータを予測することになってしまい、学習で入力された結果と同じものをそのまま返すようになってしまっています。
これ、直に「値」を予測していれば、もっとすごく当たっているような、変な結果が導かれることになりそうですね。
となると予測問題とするには、完全に切り分けるか、長い間系列を予測させ続けるか、遠い先の値を予測するかといった形になるのだろうか。
時系列って難しいですね...。
タイトルも改め、「してみたかった」に変更しました。
コメントしていただいた方、ありがとうございました。

コメント