深層強化学習でシステムトレードしてみたかった

不労所得を目指します。←

表題の通りです。

やっては見たものの、結果として、エージェントの設計により、あまり面白くない結果になってしまった感が否めないため、「してみたかった」系タイトルです。

今回は以下のアルゴリズムで、株価のデータから、システムトレードをするエージェントを学習させてみました。

• DQN
• Double DQN
• Dueling Double DQN
• Dueling Double DQN + Prioritized Experience Replay

これらのアルゴリズムについては、以前、下記の記事でも紹介しました。

PyTorchで深層強化学習（DQN、DoubleDQN）を実装してみた

以前に勉強したDeep Q-Network（DQN）を、やっぱり離散的な状態を返す簡単なゲームでなく、連続的な状態のゲームにも適用してみたいと思い、久しぶりにまた勉強しました。 最近の深層強化学習の研究を見てみたところ、DQNからさらに進化していて、A3Cなるものまで登場していましたので、少しばかりそちらについても触れてみます。

ie110704.net

2017-10-15

また、実装にはChainerを使いました。

Chainerには、深層強化学習向けに派生したライブラリとして、ChainerRLもありますが、今回も勉強のため、自分で実装してみています。

ChainerRL: https://github.com/chainer/chainerrl

また、株価のデータはKaggleのデータセット「Huge Stock Market Dataset」を使いました。

今回もKaggleのカーネルにも実装を公開しています。

kaggle kernel: https://www.kaggle.com/itoeiji/deep-reinforcement-learning-on-stock-data

GitHubにも手法ごとに下記にまとめました。

GitHub: https://github.com/Gin04gh/datascience/tree/master/kaggle_dataset_huge_stock_market_dataset

後述しますが、今回は可視化ライブラリにPlotlyを使っており、これの可視化結果はGitHub上では確認できません。

環境の作成

必要なライブラリを読み込みます。

import time
import copy
import numpy as np
import pandas as pd
import chainer
import chainer.functions as F
import chainer.links as L
from plotly import tools
from plotly.graph_objs import *
from plotly.offline import init_notebook_mode, iplot, iplot_mpl
init_notebook_mode()

可視化には、Plotlyを使ってみました。

Plotly: https://plot.ly/python/

Jupyter notebook上でも、グラフをマウスでぐりぐりと操作できるので、面白いです。

興味のある人は、Kaggleのカーネルで遊んでみて下さい。

追記（2018-04-15）

Plotlyについてまとめた記事を公開しました。

インタラクティブなグラフ生成ライブラリPlotlyについて

Plotlyというマウスでぐりぐりと動かせるようなインタラクティブなグラフを生成するライブラリがあります。 最近これをよくJupyter notebook上で可視化して遊んだりしていますので、これについてまとめます。

ie110704.net

2018-04-15

今回扱うデータについて確認します。

Huge Stock Market Datasetでは、データは銘柄ごとにファイルが分かれており、それぞれ日次の株価データが格納されています。

試しに、今回は「Google」の株価データの中身を確認してみます。

data = pd.read_csv('../input/Data/Stocks/goog.us.txt')
data['Date'] = pd.to_datetime(data['Date'])
data = data.set_index('Date')
print(data.index.min(), data.index.max())
data.head()

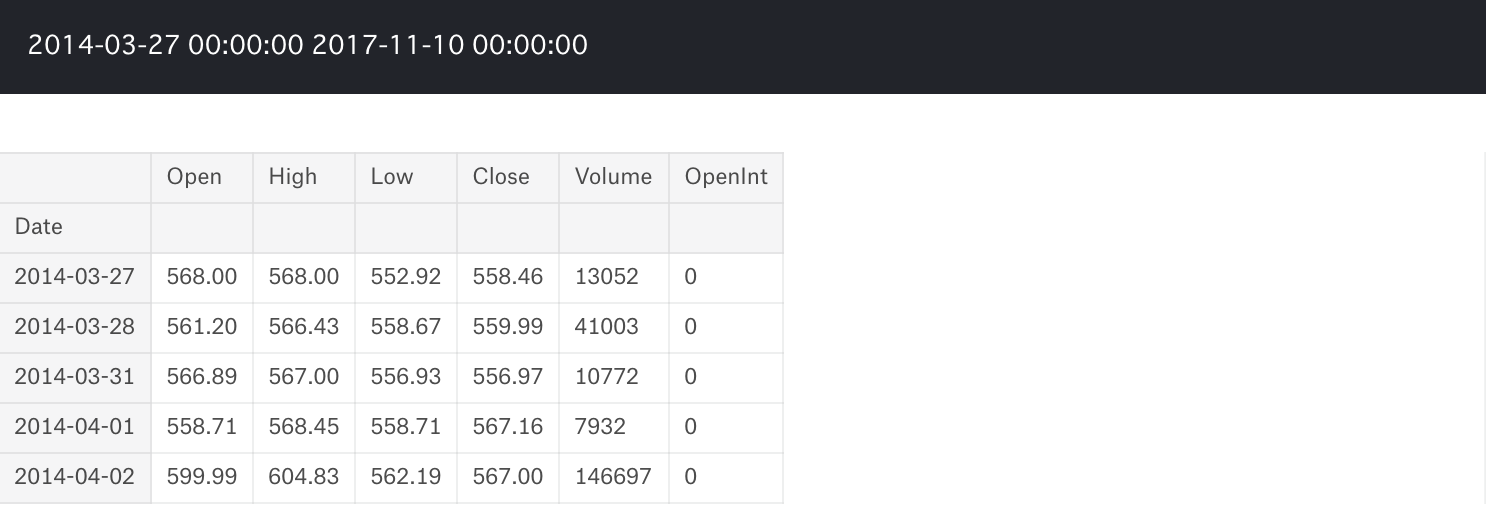
このデータを元に学習・評価をさせるため、データを学習期間と評価期間に分けます。
　

date_split = '2016-01-01'
train = data[:date_split]
test = data[date_split:]
len(train), len(test)

def plot_train_test(train, test, date_split):
    data = [
        Candlestick(x=train.index, open=train['Open'], high=train['High'], low=train['Low'], close=train['Close'], name='train'),
        Candlestick(x=test.index, open=test['Open'], high=test['High'], low=test['Low'], close=test['Close'], name='test')
    ]
    layout = {
         'shapes': [
             {'x0': date_split, 'x1': date_split, 'y0': 0, 'y1': 1, 'xref': 'x', 'yref': 'paper', 'line': {'color': 'rgb(0,0,0)', 'width': 1}}
         ],
        'annotations': [
            {'x': date_split, 'y': 1.0, 'xref': 'x', 'yref': 'paper', 'showarrow': False, 'xanchor': 'left', 'text': ' test data'},
            {'x': date_split, 'y': 1.0, 'xref': 'x', 'yref': 'paper', 'showarrow': False, 'xanchor': 'right', 'text': 'train data '}
        ]
    }
    figure = Figure(data=data, layout=layout)
    iplot(figure)

plot_train_test(train, test, date_split)

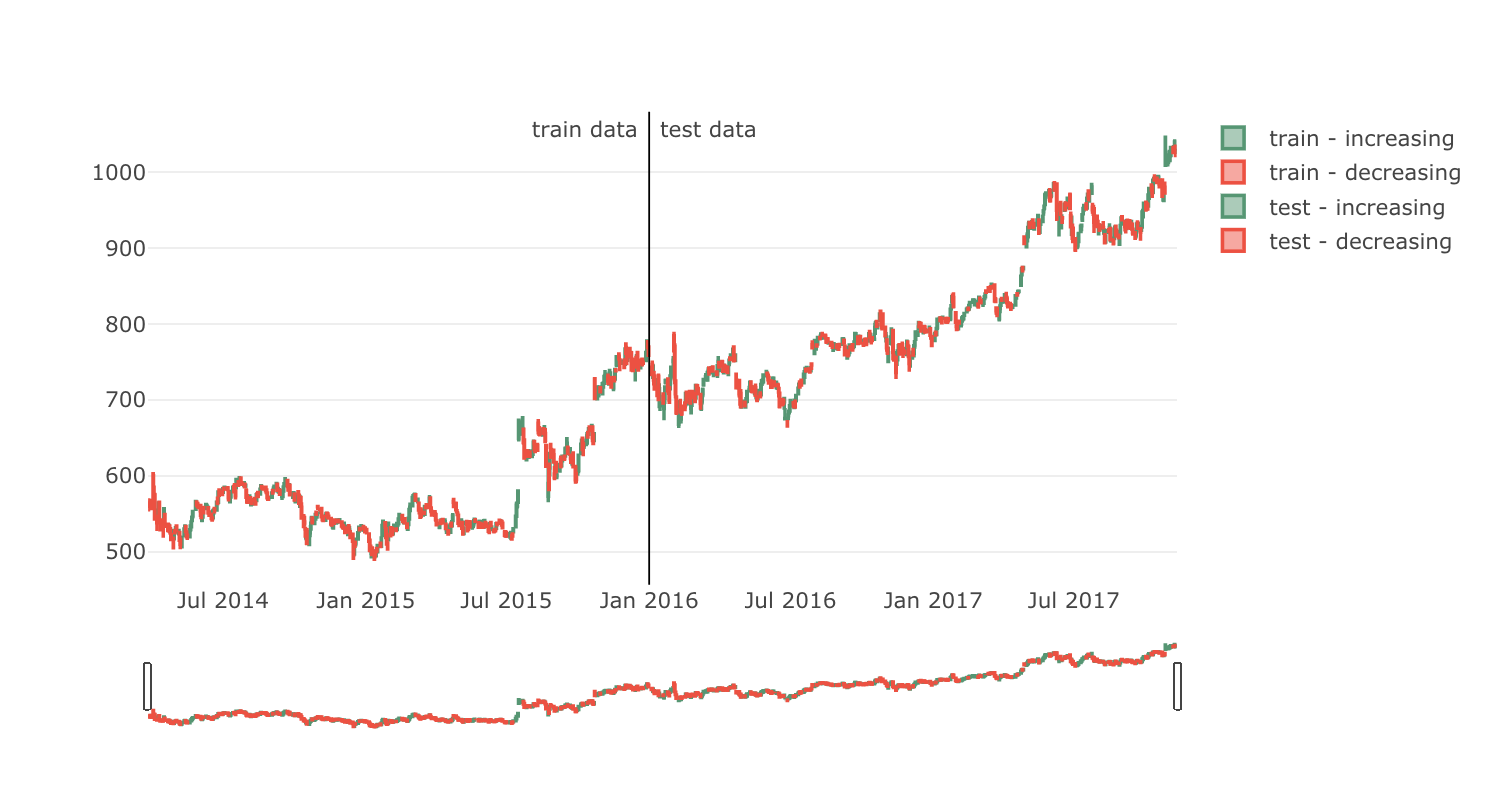
次に、強化学習を行う上では環境が必要ですので、アルゴリズム化します。

今回はまず試してみたいというレベルでしたので、下記のように非常に単純なケースを考えてみます。

• データについて
  • 日次の株価データを利用する
  • 各足の終値（Close）の値を、その日の株の売値/買値とする
  • 取引の手数料、利益にかかる税金などは考慮しない
• エージェントについて
  • 1つの銘柄を対象に取引を行う
  • エージェントは日次で「買い」「売り」「保持」のいずれかを選択する
  • 買い
    • 1度に買える株は、1株のみ
    • 買って保持できる株の数に上限は設けない
  • 売り
    • 売りを選択した場合、その時に保持している全ての株を売却する
    • 取引は現物のみ（借りて売りから入ることはできない、保持している株の数以上は売却できない）
    • 報酬の計算式
      • （現在の株価 - それぞれの買い入れ時の株価）× 保持している株の数
  • エージェントは、その日における建玉評価額を参照できる
  • エージェントは、直近90日分の株価の増減値を参照できる

これらを元に環境クラスを下記のように作ってみます。

class Environment1:
    def __init__(self, data, history_t=90):
        self.data = data
        self.history_t = history_t
        self.reset()

    def reset(self):
        self.t = 0
        self.done = False
        self.profits = 0
        self.positions = []
        self.position_value = 0
        self.history = [0 for _ in range(self.history_t)]
        return [self.position_value] + self.history # obs

    def step(self, act):
        reward = 0
        # act = 0: stay, 1: buy, 2: sell
        if act == 1:
            self.positions.append(self.data.iloc[self.t, :]['Close'])
        elif act == 2: # sell

            if len(self.positions) == 0:
                reward = -1
            else:
                profits = 0

                for p in self.positions:
                    profits += (self.data.iloc[self.t, :]['Close'] - p)

                reward += profits
                self.profits += profits
                self.positions = []

        # set next time
        self.t += 1
        self.position_value = 0

        for p in self.positions:
            self.position_value += (self.data.iloc[self.t, :]['Close'] - p)

        self.history.pop(0)
        self.history.append(self.data.iloc[self.t, :]['Close'] - self.data.iloc[(self.t-1), :]['Close'])

        # clipping reward
        if reward > 0:
            reward = 1
        elif reward < 0:
            reward = -1

        return [self.position_value] + self.history, reward, self.done # obs, reward, done

簡単なコードですので、十分に中身を追えると思います。

self.position_value は、その時に持っている株に対するその時点の損益額になり、self.history には、過去90日分の株価の増減値をリストで格納していますので、観測される状態は長さが91のベクトルということになります。

行動は、保持（何もしない）=0、買い=1、売り=2の行動数3で、売りを選択した場合に、その時の利益を報酬として受け取ります。

ちなみに最初は、破産した場合は強制終了させるという意味で done も用意していましたが、結局今回は最後まで取引させ続けてみるということで、特に使いませんでした。

参考までに、少し適当に行動させて返却値を見てみると、以下のような感じです。

env = Environment1(train)
print(env.reset())
for _ in range(3):
    pact = np.random.randint(3)
    print(env.step(pact))

実装

DQN

論文は下記になります。

Playing Atari with Deep Reinforcement Learning: https://arxiv.org/pdf/1312.5602.pdf

DQNのアルゴリズムについて、以前の記事で紹介しておりますので、こちらを参照して下さい。

PyTorchで深層強化学習（DQN、DoubleDQN）を実装してみた

以前に勉強したDeep Q-Network（DQN）を、やっぱり離散的な状態を返す簡単なゲームでなく、連続的な状態のゲームにも適用してみたいと思い、久しぶりにまた勉強しました。 最近の深層強化学習の研究を見てみたところ、DQNからさらに進化していて、A3Cなるものまで登場していましたので、少しばかりそちらについても触れてみます。

ie110704.net

2017-10-15

Chainerで実装した結果が下記のコードになります。

# DQN
def train_dqn(env):
    class Q_Network(chainer.Chain):
        def __init__(self, input_size, hidden_size, output_size):
            super(Q_Network, self).__init__(
                fc1 = L.Linear(input_size, hidden_size),
                fc2 = L.Linear(hidden_size, hidden_size),
                fc3 = L.Linear(hidden_size, output_size)
            )

        def __call__(self, x):
            h = F.relu(self.fc1(x))
            h = F.relu(self.fc2(h))
            y = self.fc3(h)
            return y

        def reset(self):
            self.zerograds()

    Q = Q_Network(input_size=env.history_t+1, hidden_size=100, output_size=3)
    Q_ast = copy.deepcopy(Q)

    optimizer = chainer.optimizers.Adam()
    optimizer.setup(Q)

    epoch_num = 50
    step_max = len(env.data)-1
    memory_size = 200
    batch_size = 20
    epsilon = 1.0
    epsilon_decrease = 1e-3
    epsilon_min = 0.1
    start_reduce_epsilon = 200
    train_freq = 10
    update_q_freq = 20
    gamma = 0.97
    show_log_freq = 5
    memory = []
    total_step = 0
    total_rewards = []
    total_losses = []

    start = time.time()
    for epoch in range(epoch_num):
        pobs = env.reset()
        step = 0
        done = False

        total_reward = 0
        total_loss = 0
        while not done and step < step_max:
            # select act
            pact = np.random.randint(3)

            if np.random.rand() > epsilon:
                pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
                pact = np.argmax(pact.data)

            # act
            obs, reward, done = env.step(pact)

            # add memory
            memory.append((pobs, pact, reward, obs, done))
            if len(memory) > memory_size:
                memory.pop(0)

            # train or update q
            if len(memory) == memory_size:
                if total_step % train_freq == 0:
                    shuffled_memory = np.random.permutation(memory)
                    memory_idx = range(len(shuffled_memory))

                    for i in memory_idx[::batch_size]:
                        batch = np.array(shuffled_memory[i:i+batch_size])
                        b_pobs = np.array(batch[:, 0].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_pact = np.array(batch[:, 1].tolist(), dtype=np.int32)
                        b_reward = np.array(batch[:, 2].tolist(), dtype=np.int32)
                        b_obs = np.array(batch[:, 3].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_done = np.array(batch[:, 4].tolist(), dtype=np.bool)

                        q = Q(b_pobs)
                        maxq = np.max(Q_ast(b_obs).data, axis=1)
                        target = copy.deepcopy(q.data)
                        for j in range(batch_size):
                            target[j, b_pact[j]] = b_reward[j]+gamma*maxq[j]*(not b_done[j])

                        Q.reset()
                        loss = F.mean_squared_error(q, target)
                        total_loss += loss.data
                        loss.backward()
                        optimizer.update()

                if total_step % update_q_freq == 0:
                    Q_ast = copy.deepcopy(Q)

            # epsilon
            if epsilon > epsilon_min and total_step > start_reduce_epsilon:
                epsilon -= epsilon_decrease

            # next step
            total_reward += reward
            pobs = obs
            step += 1
            total_step += 1

        total_rewards.append(total_reward)
        total_losses.append(total_loss)
        if (epoch+1) % show_log_freq == 0:
            log_reward = sum(total_rewards[((epoch+1)-show_log_freq):])/show_log_freq
            log_loss = sum(total_losses[((epoch+1)-show_log_freq):])/show_log_freq
            elapsed_time = time.time()-start
            print('\t'.join(map(str, [epoch+1, epsilon, total_step, log_reward, log_loss, elapsed_time])))
            start = time.time()

    return Q, total_losses, total_rewards

これを学習させてみて、エポックごとにロスと報酬がどのように推移していくか、確認してみます。

Q, total_losses, total_rewards = train_dqn(Environment1(train))

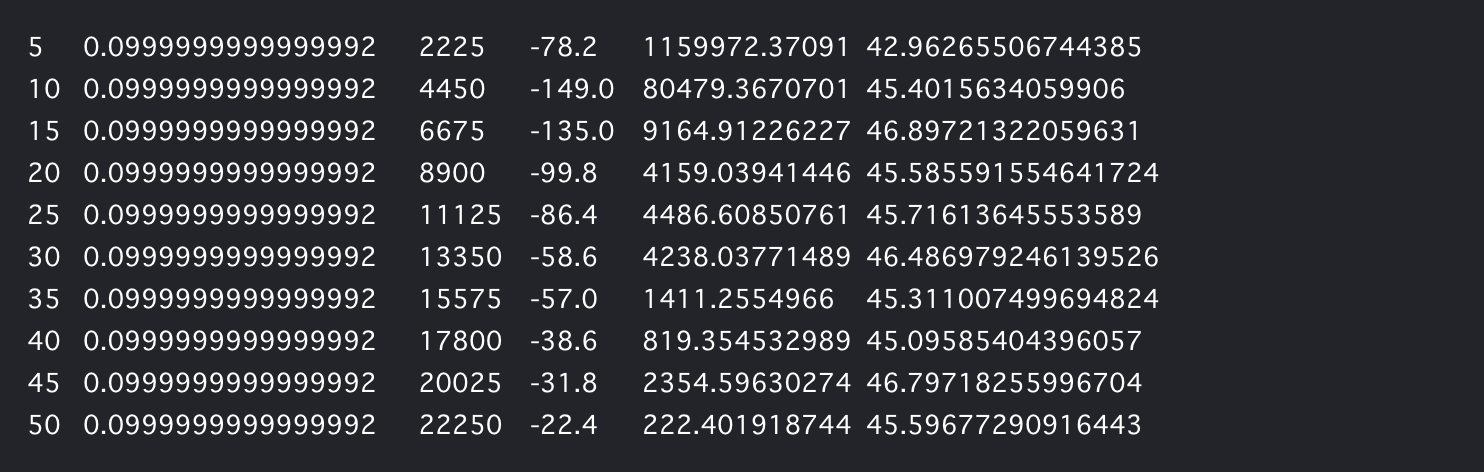
def plot_loss_reward(total_losses, total_rewards):
    figure = tools.make_subplots(rows=1, cols=2, subplot_titles=('loss', 'reward'), print_grid=False)
    figure.append_trace(Scatter(y=total_losses, mode='lines', line=dict(color='skyblue')), 1, 1)
    figure.append_trace(Scatter(y=total_rewards, mode='lines', line=dict(color='orange')), 1, 2)
    figure['layout']['xaxis1'].update(title='epoch')
    figure['layout']['xaxis2'].update(title='epoch')
    figure['layout'].update(height=400, width=900, showlegend=False)
    iplot(figure)

plot_loss_reward(total_losses, total_rewards)

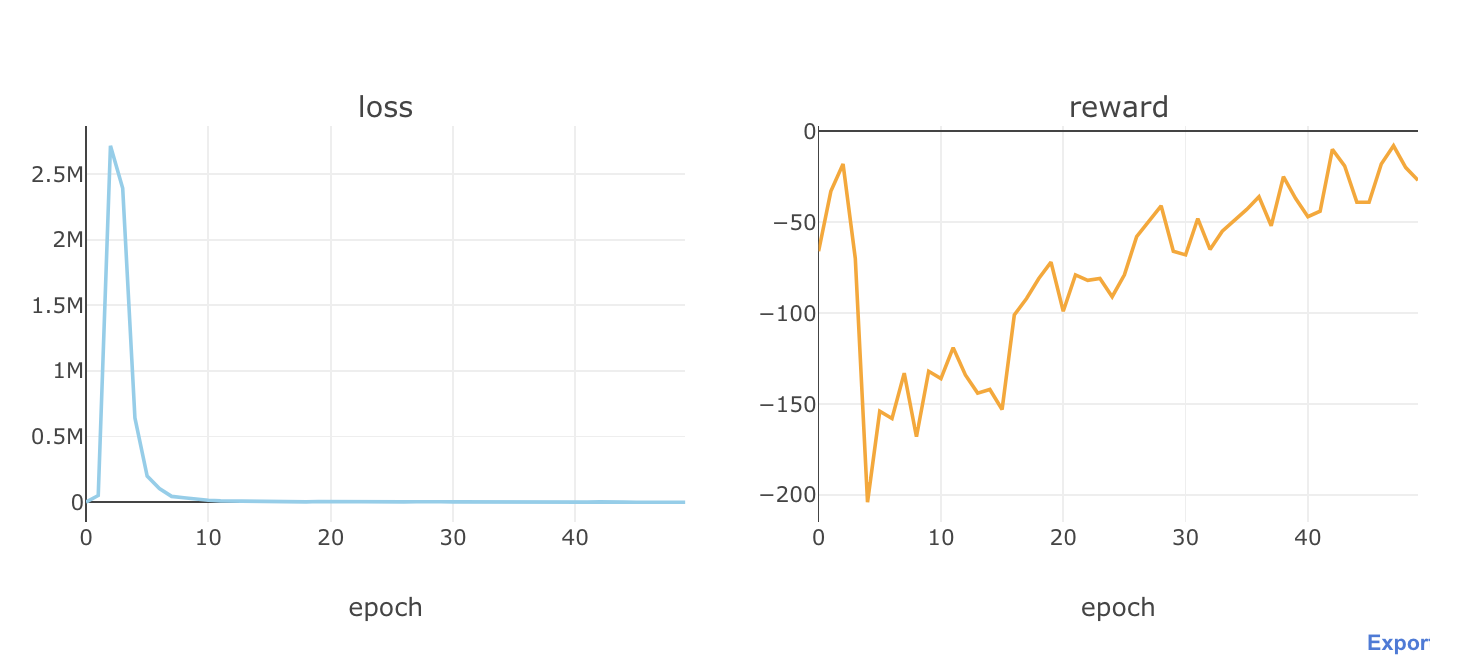
めっちゃ利益マイナスで、だんだんと被害額を抑えているようです笑

何やらあまりうまく行っていないようですが、学習・評価データで、学習した 関数を用いて行動させてみます。

def plot_train_test_by_q(train_env, test_env, Q, algorithm_name):
    # train
    pobs = train_env.reset()

    train_acts = []
    train_rewards = []
    for _ in range(len(train_env.data)-1):
        pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
        pact = np.argmax(pact.data)
        train_acts.append(pact)
        obs, reward, done = train_env.step(pact)
        train_rewards.append(reward)
        pobs = obs

    train_profits = train_env.profits

    # test
    pobs = test_env.reset()
    test_acts = []
    test_rewards = []
    for _ in range(len(test_env.data)-1):
        pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
        pact = np.argmax(pact.data)
        test_acts.append(pact)
        obs, reward, done = test_env.step(pact)
        test_rewards.append(reward)
        pobs = obs

    test_profits = test_env.profits

    # plot
    train_copy = train_env.data.copy()
    test_copy = test_env.data.copy()
    train_copy['act'] = train_acts + [np.nan]
    train_copy['reward'] = train_rewards + [np.nan]
    test_copy['act'] = test_acts + [np.nan]
    test_copy['reward'] = test_rewards + [np.nan]

    train0 = train_copy[train_copy['act'] == 0]
    train1 = train_copy[train_copy['act'] == 1]
    train2 = train_copy[train_copy['act'] == 2]

    test0 = test_copy[test_copy['act'] == 0]
    test1 = test_copy[test_copy['act'] == 1]
    test2 = test_copy[test_copy['act'] == 2]

    act_color0, act_color1, act_color2 = 'gray', 'cyan', 'magenta'
    data = [
        Candlestick(x=train0.index, open=train0['Open'], high=train0['High'], low=train0['Low'], close=train0['Close'], increasing=dict(line=dict(color=act_color0)), decreasing=dict(line=dict(color=act_color0))),
        Candlestick(x=train1.index, open=train1['Open'], high=train1['High'], low=train1['Low'], close=train1['Close'], increasing=dict(line=dict(color=act_color1)), decreasing=dict(line=dict(color=act_color1))),
        Candlestick(x=train2.index, open=train2['Open'], high=train2['High'], low=train2['Low'], close=train2['Close'], increasing=dict(line=dict(color=act_color2)), decreasing=dict(line=dict(color=act_color2))),
        Candlestick(x=test0.index, open=test0['Open'], high=test0['High'], low=test0['Low'], close=test0['Close'], increasing=dict(line=dict(color=act_color0)), decreasing=dict(line=dict(color=act_color0))),
        Candlestick(x=test1.index, open=test1['Open'], high=test1['High'], low=test1['Low'], close=test1['Close'], increasing=dict(line=dict(color=act_color1)), decreasing=dict(line=dict(color=act_color1))),
        Candlestick(x=test2.index, open=test2['Open'], high=test2['High'], low=test2['Low'], close=test2['Close'], increasing=dict(line=dict(color=act_color2)), decreasing=dict(line=dict(color=act_color2)))
    ]
    title = '{}: train s-reward {}, profits {}, test s-reward {}, profits {}'.format(
        algorithm_name,
        int(sum(train_rewards)),
        int(train_profits),
        int(sum(test_rewards)),
        int(test_profits)
    )
    layout = {
        'title': title,
        'showlegend': False,
         'shapes': [
             {'x0': date_split, 'x1': date_split, 'y0': 0, 'y1': 1, 'xref': 'x', 'yref': 'paper', 'line': {'color': 'rgb(0,0,0)', 'width': 1}}
         ],
        'annotations': [
            {'x': date_split, 'y': 1.0, 'xref': 'x', 'yref': 'paper', 'showarrow': False, 'xanchor': 'left', 'text': ' test data'},
            {'x': date_split, 'y': 1.0, 'xref': 'x', 'yref': 'paper', 'showarrow': False, 'xanchor': 'right', 'text': 'train data '}
        ]
    }
    figure = Figure(data=data, layout=layout)
    iplot(figure)

plot_train_test_by_q(Environment1(train), Environment1(test), Q, 'DQN')

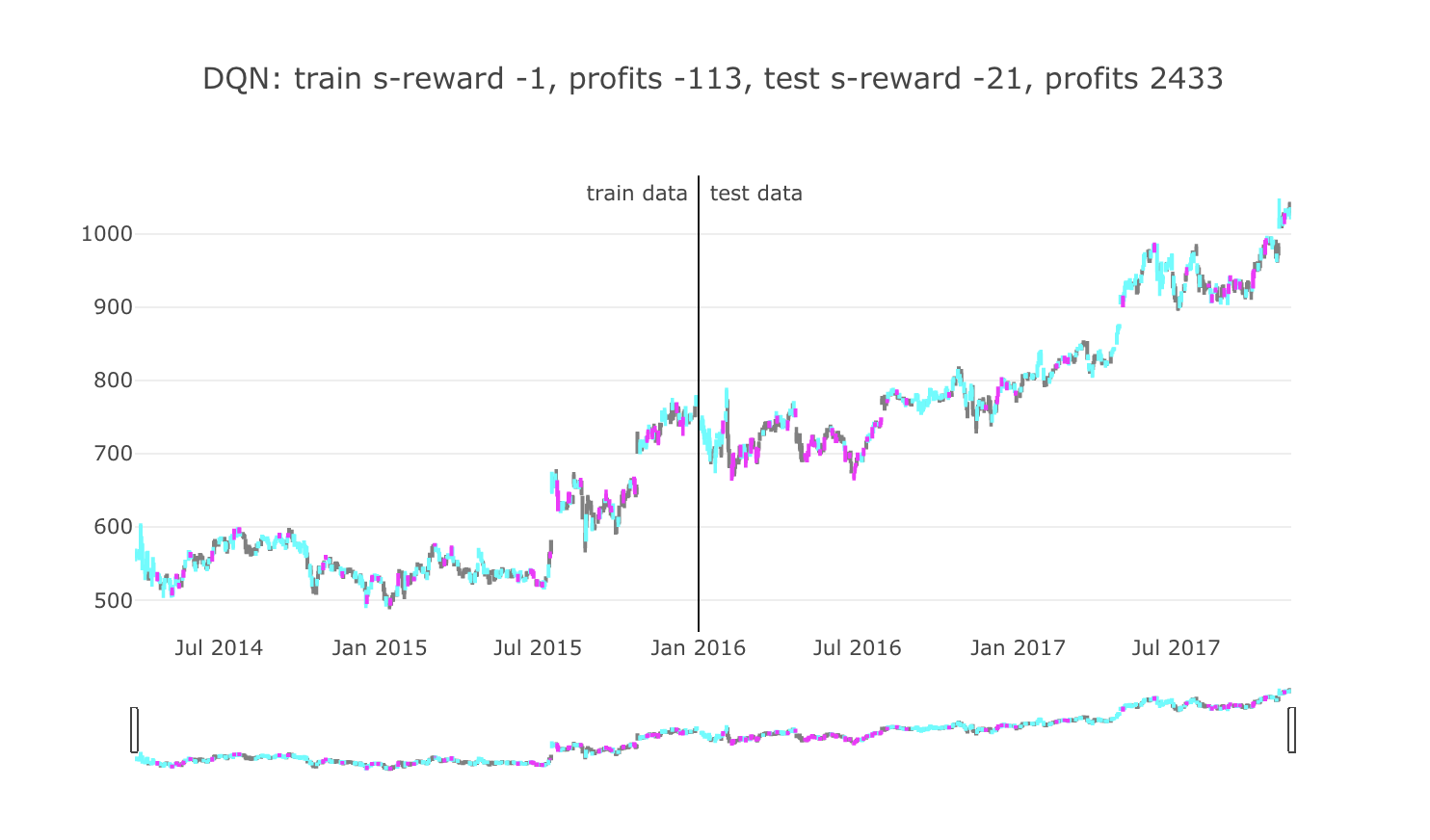
毎日エージェントが何かしら行動をしますので、色を分けて行動を可視化させてみました。

ローソク足の色が、グレーは「保持」（何もしなかった）、シアンは「買い」、マゼンタは「売り」を表しています。

タイトル部分に、学習データ期間と評価データ期間で分けて成績を書いています。

環境の設計により、報酬はクリッピングされていますので、s-reward は報酬の「+1」や「-1」を繰り返し取得した後の合計となります。

profits は実際の株価の価格で最終的な損益価格を表しています。

評価データでは最終的にプラスの利益を出していますが、何かあまり、意味のある行動を学習したようには見えませんでした。

Double DQN

深層強化学習のアルゴリズムを改良してみます。

論文は下記になります。

Deep reinforcement learning with double q-learning: https://arxiv.org/pdf/1509.06461.pdf

Double DQNでは、教師信号の作成に、パラメータを固定している と学習中の の両方を使います。

DQNでの教師信号：

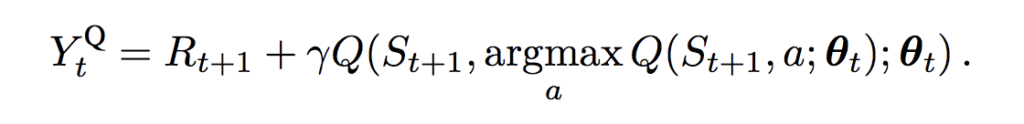
Double DQNでの教師信号:

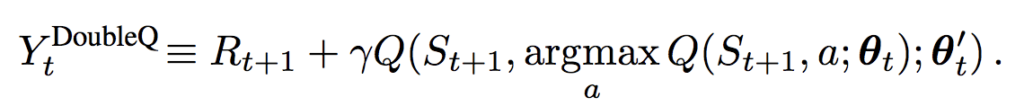
実装は下記になります。

# Double DQN
def train_ddqn(env):
    class Q_Network(chainer.Chain):
        def __init__(self, input_size, hidden_size, output_size):
            super(Q_Network, self).__init__(
                fc1 = L.Linear(input_size, hidden_size),
                fc2 = L.Linear(hidden_size, hidden_size),
                fc3 = L.Linear(hidden_size, output_size)
            )

        def __call__(self, x):
            h = F.relu(self.fc1(x))
            h = F.relu(self.fc2(h))
            y = self.fc3(h)
            return y

        def reset(self):
            self.zerograds()

    Q = Q_Network(input_size=env.history_t+1, hidden_size=100, output_size=3)
    Q_ast = copy.deepcopy(Q)

    optimizer = chainer.optimizers.Adam()
    optimizer.setup(Q)

    epoch_num = 50
    step_max = len(env.data)-1
    memory_size = 200
    batch_size = 50
    epsilon = 1.0
    epsilon_decrease = 1e-3
    epsilon_min = 0.1
    start_reduce_epsilon = 200
    train_freq = 10
    update_q_freq = 20
    gamma = 0.97
    show_log_freq = 5
    memory = []
    total_step = 0
    total_rewards = []
    total_losses = []

    start = time.time()
    for epoch in range(epoch_num):
        pobs = env.reset()
        step = 0
        done = False

        total_reward = 0
        total_loss = 0
        while not done and step < step_max:
            # select act
            pact = np.random.randint(3)

            if np.random.rand() > epsilon:
                pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
                pact = np.argmax(pact.data)

            # act
            obs, reward, done = env.step(pact)

            # add memory
            memory.append((pobs, pact, reward, obs, done))
            if len(memory) > memory_size:
                memory.pop(0)

            # train or update q
            if len(memory) == memory_size:
                if total_step % train_freq == 0:
                    shuffled_memory = np.random.permutation(memory)
                    memory_idx = range(len(shuffled_memory))

                    for i in memory_idx[::batch_size]:
                        batch = np.array(shuffled_memory[i:i+batch_size])
                        b_pobs = np.array(batch[:, 0].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_pact = np.array(batch[:, 1].tolist(), dtype=np.int32)
                        b_reward = np.array(batch[:, 2].tolist(), dtype=np.int32)
                        b_obs = np.array(batch[:, 3].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_done = np.array(batch[:, 4].tolist(), dtype=np.bool)

                        q = Q(b_pobs)
                        indices = np.argmax(q.data, axis=1)
                        maxqs = Q_ast(b_obs).data
                        target = copy.deepcopy(q.data)
                        for j in range(batch_size):
                            target[j, b_pact[j]] = b_reward[j]+gamma*maxqs[j, indices[j]]*(not b_done[j])

                        Q.reset()
                        loss = F.mean_squared_error(q, target)
                        total_loss += loss.data
                        loss.backward()
                        optimizer.update()

                if total_step % update_q_freq == 0:
                    Q_ast = copy.deepcopy(Q)

            # epsilon
            if epsilon > epsilon_min and total_step > start_reduce_epsilon:
                epsilon -= epsilon_decrease

            # next step
            total_reward += reward
            pobs = obs
            step += 1
            total_step += 1

        total_rewards.append(total_reward)
        total_losses.append(total_loss)
        if (epoch+1) % show_log_freq == 0:
            log_reward = sum(total_rewards[((epoch+1)-show_log_freq):])/show_log_freq
            log_loss = sum(total_losses[((epoch+1)-show_log_freq):])/show_log_freq
            elapsed_time = time.time()-start
            print('\t'.join(map(str, [epoch+1, epsilon, total_step, log_reward, log_loss, elapsed_time])))
            start = time.time()

    return Q, total_losses, total_rewards

論文の数式を見れば分かるように、DQNからアルゴリズムとして変更する部分は多くなく、

q = Q(b_pobs)
maxq = np.max(Q_ast(b_obs).data, axis=1)
target = copy.deepcopy(q.data)
for j in range(batch_size):
    target[j, b_pact[j]] = b_reward[j]+gamma*maxq[j]*(not b_done[j])

Q.reset()
loss = F.mean_squared_error(q, target)
total_loss += loss.data
loss.backward()
optimizer.update()

の部分を

q = Q(b_pobs)
indices = np.argmax(q.data, axis=1)
maxqs = Q_ast(b_obs).data
target = copy.deepcopy(q.data)
for j in range(batch_size):
    target[j, b_pact[j]] = b_reward[j]+gamma*maxqs[j, indices[j]]*(not b_done[j])

Q.reset()
loss = F.mean_squared_error(q, target)
total_loss += loss.data
loss.backward()
optimizer.update()

とするだけで実現できます。

学習をさせてみた結果は下記になります。

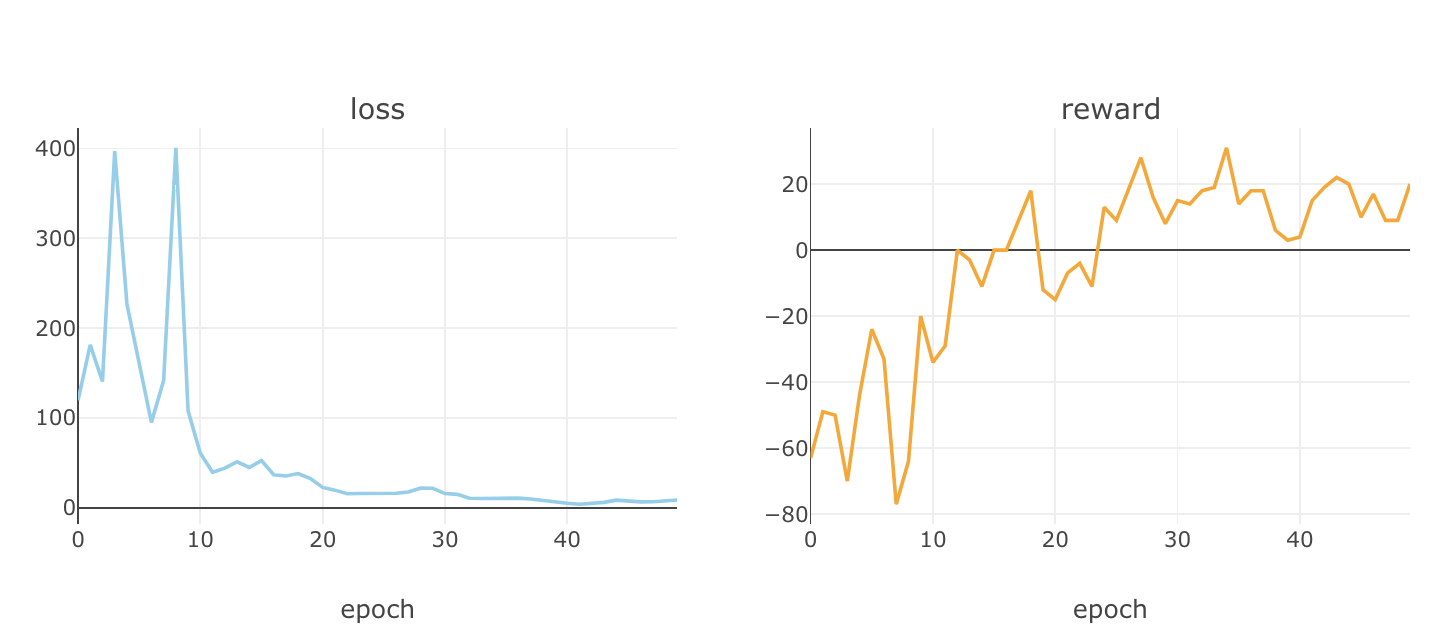
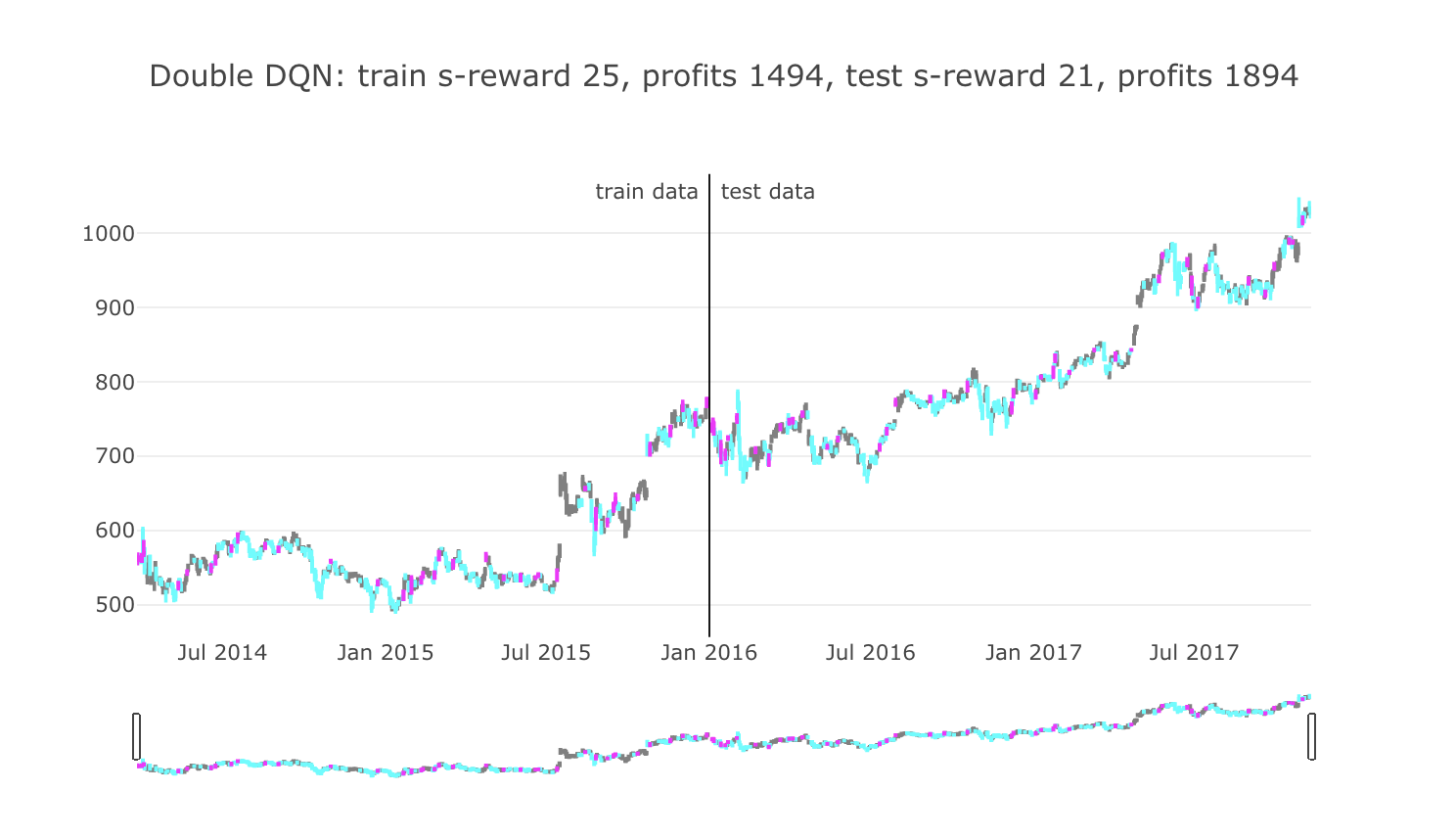
利益を出すようになりました。

が、この時点で「あ」と思ってしまいます。

「これは、とりあえず買っておいて、評価がプラスになったら売るというのを繰り返しているだけじゃ...」

そう考えると、エージェントの設計から、そりゃそう行動するように学習してしまうよな、と余計に感じてしまいましたが、ひとまず次のアルゴリズムに行ってみます。

Dueling Double DQN

論文は下記になります。

Dueling Network Architectures for Deep Reinforcement Learning: https://arxiv.org/pdf/1511.06581.pdf

DQNやDouble DQNでは、 関数の更新は、1回につき、1つの行動に対してのみ更新するようになっていました。

これを下記のように、 関数を状態価値関数 とAdvantage（行動優位）関数 に分解して学習させることで、状態価値観数については毎回更新できることで、結果として収束が早くなります。

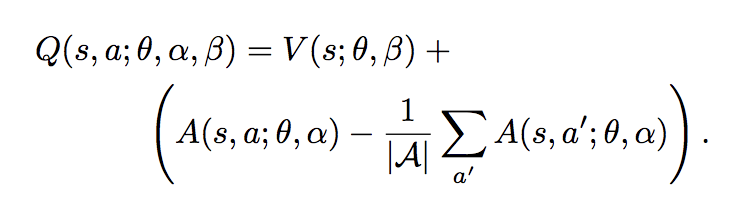
実装は下記になります。

# Dueling Double DQN
def train_dddqn(env):
    class Q_Network(chainer.Chain):
        def __init__(self, input_size, hidden_size, output_size):
            super(Q_Network, self).__init__(
                fc1 = L.Linear(input_size, hidden_size),
                fc2 = L.Linear(hidden_size, hidden_size),
                fc3 = L.Linear(hidden_size, hidden_size//2),
                fc4 = L.Linear(hidden_size, hidden_size//2),
                state_value = L.Linear(hidden_size//2, 1),
                advantage_value = L.Linear(hidden_size//2, output_size)
            )
            self.input_size = input_size
            self.hidden_size = hidden_size
            self.output_size = output_size

        def __call__(self, x):
            h = F.relu(self.fc1(x))
            h = F.relu(self.fc2(h))
            hs = F.relu(self.fc3(h))
            ha = F.relu(self.fc4(h))
            state_value = self.state_value(hs)
            advantage_value = self.advantage_value(ha)
            advantage_mean = (F.sum(advantage_value, axis=1)/float(self.output_size)).reshape(-1, 1)
            q_value = F.concat([state_value for _ in range(self.output_size)], axis=1) + (advantage_value - F.concat([advantage_mean for _ in range(self.output_size)], axis=1))
            return q_value

        def reset(self):
            self.zerograds()

    Q = Q_Network(input_size=env.history_t+1, hidden_size=100, output_size=3)
    Q_ast = copy.deepcopy(Q)

    optimizer = chainer.optimizers.Adam()
    optimizer.setup(Q)

    epoch_num = 50
    step_max = len(env.data)-1
    memory_size = 200
    batch_size = 50
    epsilon = 1.0
    epsilon_decrease = 1e-3
    epsilon_min = 0.1
    start_reduce_epsilon = 200
    train_freq = 10
    update_q_freq = 20
    gamma = 0.97
    show_log_freq = 5
    memory = []
    total_step = 0
    total_rewards = []
    total_losses = []

    start = time.time()
    for epoch in range(epoch_num):
        pobs = env.reset()
        step = 0
        done = False

        total_reward = 0
        total_loss = 0
        while not done and step < step_max:
            # select act
            pact = np.random.randint(3)
            if np.random.rand() > epsilon:
                pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
                pact = np.argmax(pact.data)

            # act
            obs, reward, done = env.step(pact)

            # add memory
            memory.append((pobs, pact, reward, obs, done))
            if len(memory) > memory_size:
                memory.pop(0)

            # train or update q
            if len(memory) == memory_size:
                if total_step % train_freq == 0:
                    shuffled_memory = np.random.permutation(memory)
                    memory_idx = range(len(shuffled_memory))

                    for i in memory_idx[::batch_size]:
                        batch = np.array(shuffled_memory[i:i+batch_size])
                        b_pobs = np.array(batch[:, 0].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_pact = np.array(batch[:, 1].tolist(), dtype=np.int32)
                        b_reward = np.array(batch[:, 2].tolist(), dtype=np.int32)
                        b_obs = np.array(batch[:, 3].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_done = np.array(batch[:, 4].tolist(), dtype=np.bool)

                        q = Q(b_pobs)
                        indices = np.argmax(q.data, axis=1)
                        maxqs = Q_ast(b_obs).data
                        target = copy.deepcopy(q.data)
                        for j in range(batch_size):
                            target[j, b_pact[j]] = b_reward[j]+gamma*maxqs[j, indices[j]]*(not b_done[j])

                        Q.reset()
                        loss = F.mean_squared_error(q, target)
                        total_loss += loss.data
                        loss.backward()
                        optimizer.update()

                if total_step % update_q_freq == 0:
                    Q_ast = copy.deepcopy(Q)

            # epsilon
            if epsilon > epsilon_min and total_step > start_reduce_epsilon:
                epsilon -= epsilon_decrease

            # next step
            total_reward += reward
            pobs = obs
            step += 1
            total_step += 1

        total_rewards.append(total_reward)
        total_losses.append(total_loss)
        if (epoch+1) % show_log_freq == 0:
            log_reward = sum(total_rewards[((epoch+1)-show_log_freq):])/show_log_freq
            log_loss = sum(total_losses[((epoch+1)-show_log_freq):])/show_log_freq
            elapsed_time = time.time()-start
            print('\t'.join(map(str, [epoch+1, epsilon, total_step, log_reward, log_loss, elapsed_time])))
            start = time.time()

    return Q, total_losses, total_rewards

学習のアルゴリズムに関しては、DQNやDouble DQNの時と変更する必要がありませんので、 関数のみを上記のようにごっそり変更すればOKです。

用意するレイヤーについては問題ないと思いますが、順伝播のところで、上記の論文の数式を実行するように色々とやっています。

学習をさせてみましたところ、

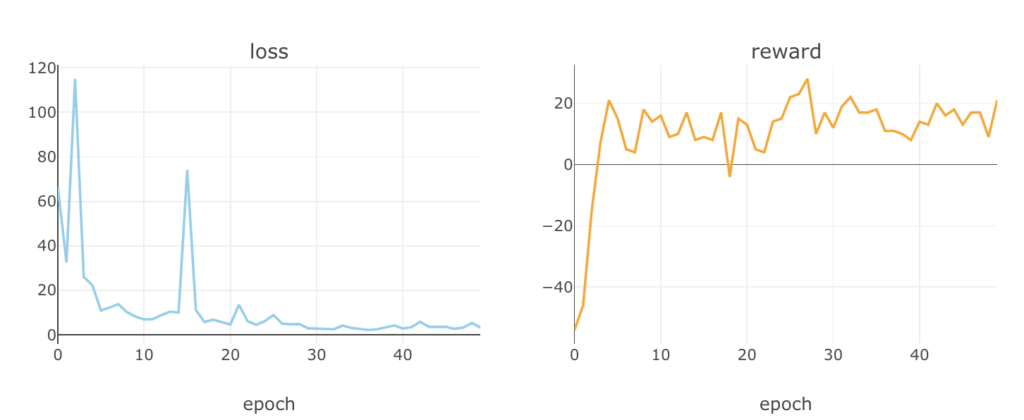
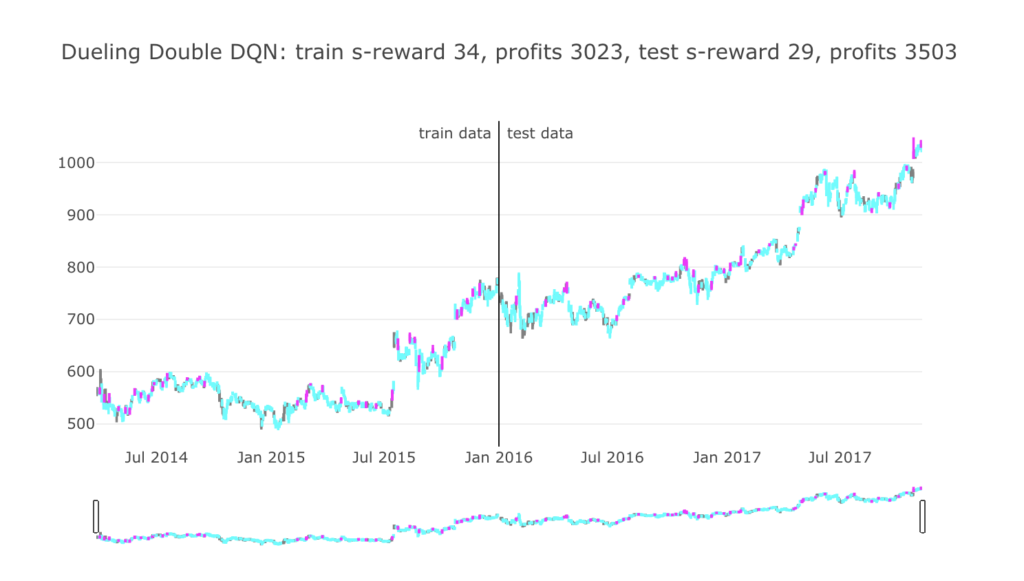
とにかく買いまくって上がったら売るを永遠と繰り返しています。

シミュレーションの設計をちゃんとやるべきであったなーと反省です。

ひとまずアルゴリズムの勉強をしたく、最後までやっちゃいます。

Prioritized Experience Replay

論文は下記になります。

Prioritized Experience Replay: https://arxiv.org/pdf/1511.05952.pdf

Experience Replayでは、経験からランダムに選んで学習してきています。

そこで、より学習に役立つ経験を優先して学習させたいというモチベーションが発生します。

経験サンプルの重要性 を、TD誤差の絶対値 （パラメータの更新幅とみなせる）を用いて表して、経験サンプリングすることを考え、TD誤差の大きい経験を優先して学習させられるようにします。

経験サンプリングに関しては若干ややこしいのですが、どうやら、

1. TD誤差の大きい経験を降順に並べる
2. バッチサイズ分、降順に並べた経験を区切る
3. それぞれの区間から適当に経験を選ぶ

ということを考えるようです。

実装は下記になります。

# Dueling Double DQN + Prioritized Experience Replay
def train_dddqn_per(env):
    class Q_Network(chainer.Chain):
        def __init__(self, input_size, hidden_size, output_size):
            super(Q_Network, self).__init__(
                fc1 = L.Linear(input_size, hidden_size),
                fc2 = L.Linear(hidden_size, hidden_size),
                fc3 = L.Linear(hidden_size, hidden_size//2),
                fc4 = L.Linear(hidden_size, hidden_size//2),
                state_value = L.Linear(hidden_size//2, 1),
                advantage_value = L.Linear(hidden_size//2, output_size)
            )
            self.input_size = input_size
            self.hidden_size = hidden_size
            self.output_size = output_size

        def __call__(self, x):
            h = F.relu(self.fc1(x))
            h = F.relu(self.fc2(h))
            hs = F.relu(self.fc3(h))
            ha = F.relu(self.fc4(h))
            state_value = self.state_value(hs)
            advantage_value = self.advantage_value(ha)
            advantage_mean = (F.sum(advantage_value, axis=1)/float(self.output_size)).reshape(-1, 1)
            q_value = F.concat([state_value for _ in range(self.output_size)], axis=1) + (advantage_value - F.concat([advantage_mean for _ in range(self.output_size)], axis=1))
            return q_value

        def reset(self):
            self.zerograds()

    Q = Q_Network(input_size=env.history_t+1, hidden_size=100, output_size=3)
    Q_ast = copy.deepcopy(Q)

    optimizer = chainer.optimizers.Adam()
    optimizer.setup(Q)

    epoch_num = 50
    step_max = len(env.data)-1
    memory_size = 200
    batch_size = 50
    epsilon = 1.0
    epsilon_decrease = 1e-3
    epsilon_min = 0.1
    start_reduce_epsilon = 200
    train_freq = 10
    update_q_freq = 20
    gamma = 0.97
    show_log_freq = 5
    memory = []
    total_step = 0
    total_rewards = []
    total_losses = []

    start = time.time()
    for epoch in range(epoch_num):
        pobs = env.reset()
        step = 0
        done = False

        total_reward = 0
        total_loss = 0
        while not done and step < step_max:
            # select act
            pact = np.random.randint(3)
            if np.random.rand() > epsilon:
                pact = Q(np.array(pobs, dtype=np.float32).reshape(1, -1))
                pact = np.argmax(pact.data)

            # act
            obs, reward, done = env.step(pact)

            # add memory
            memory.append((pobs, pact, reward, obs, done))
            if len(memory) > memory_size:
                memory.pop(0)

            # train or update q
            if len(memory) == memory_size:
                if total_step % train_freq == 0:
                    for _ in range(memory_size//batch_size):
                        memory_ = np.array(memory)
                        m_pobs = np.array(memory_[:, 0].tolist(), dtype=np.float32).reshape(memory_size, -1)
                        m_pact = np.array(memory_[:, 1].tolist(), dtype=np.int32)
                        m_reward = np.array(memory_[:, 2].tolist(), dtype=np.int32)
                        m_obs = np.array(memory_[:, 3].tolist(), dtype=np.float32).reshape(memory_size, -1)
                        priorities = np.zeros(memory_size)

                        q = Q(m_pobs).data
                        indices = np.argmax(q, axis=1)
                        maxqs = Q_ast(m_obs).data
                        for j in range(memory_size):
                            td_error = m_reward[j]+gamma*maxqs[j, indices[j]]-q[j, m_pact[j]]
                            priorities[j] = abs(td_error)

                        memory_idx = [np.random.choice(k, 1)[0] for k in np.array_split(np.argsort(priorities)[::-1], batch_size)]
                        batch = np.array([memory[i] for i in memory_idx])
                        b_pobs = np.array(batch[:, 0].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_pact = np.array(batch[:, 1].tolist(), dtype=np.int32)
                        b_reward = np.array(batch[:, 2].tolist(), dtype=np.int32)
                        b_obs = np.array(batch[:, 3].tolist(), dtype=np.float32).reshape(batch_size, -1)
                        b_done = np.array(batch[:, 4].tolist(), dtype=np.bool)

                        q = Q(b_pobs)
                        indices = np.argmax(q.data, axis=1)
                        maxqs = Q_ast(b_obs).data
                        target = copy.deepcopy(q.data)
                        for j in range(batch_size):
                            target[j, b_pact[j]] = b_reward[j]+gamma*maxqs[j, indices[j]]*(not b_done[j])

                        Q.reset()
                        loss = F.mean_squared_error(q, target)
                        total_loss += loss.data
                        loss.backward()
                        optimizer.update()

                if total_step % update_q_freq == 0:
                    Q_ast = copy.deepcopy(Q)

            # epsilon
            if epsilon > epsilon_min and total_step > start_reduce_epsilon:
                epsilon -= epsilon_decrease

            # next step
            total_reward += reward
            pobs = obs
            step += 1
            total_step += 1
        total_rewards.append(total_reward)
        total_losses.append(total_loss)

        if (epoch+1) % show_log_freq == 0:
            log_reward = sum(total_rewards[((epoch+1)-show_log_freq):])/show_log_freq
            log_loss = sum(total_losses[((epoch+1)-show_log_freq):])/show_log_freq
            elapsed_time = time.time()-start
            print('\t'.join(map(str, [epoch+1, epsilon, total_step, log_reward, log_loss, elapsed_time])))
            start = time.time()

    return Q, total_losses, total_rewards

学習させてみた結果、

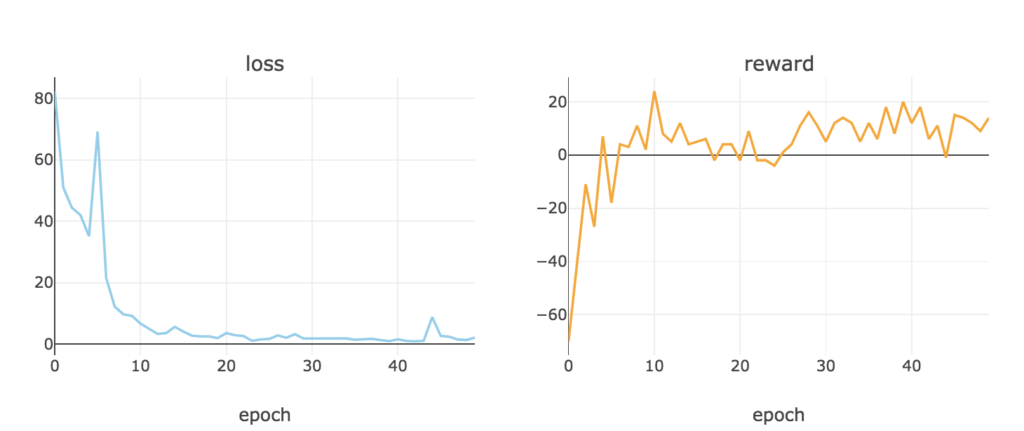
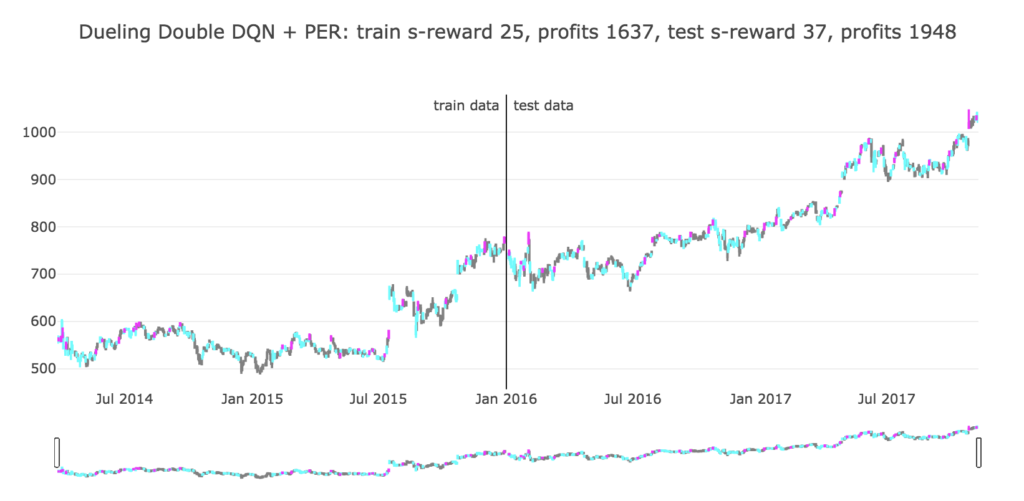
若干成績が落ちましたが、変わらず、とりあえず買っておいて上がったら売るを繰り返しているようです。

ちょいちょい保持を選択しているのはなぜでしょうか。

その他のデータでの結果

これまでの感想通り、結果としては、ルールベース的な学習をしてしまったようでした。

ただ、今回のGoogleの株価は、ずっと上昇傾向にありましたので、もしかしたらランダムな行動を取っても、割りと利益を出しそうな気もします。

そこで、そうでない株価データも学習させてみた場合の様子についても、確認してみました。

1. Twitter

1つ目はTwitterの株価データです。

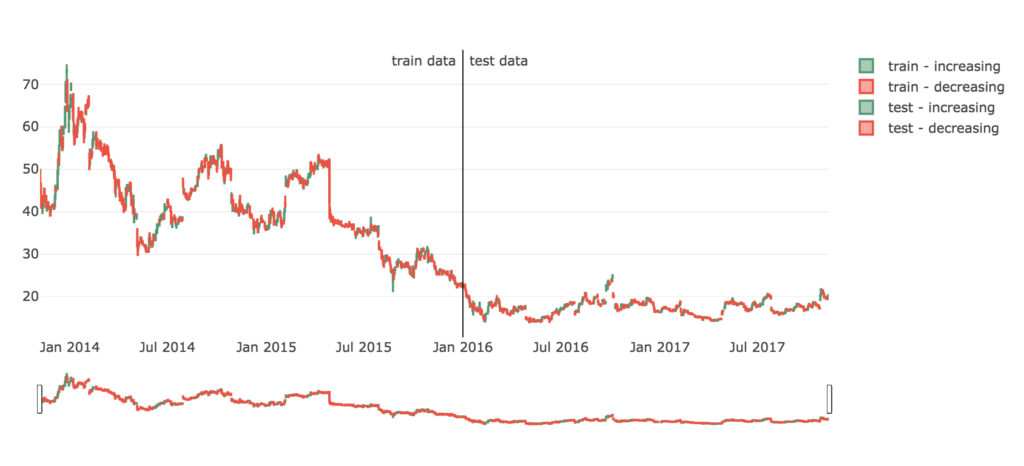
下降傾向です。かなしい。←

こんな中でもちゃんと上がったタイミングで売ることができるのでしょうか。

学習させてみた結果が以下になります。

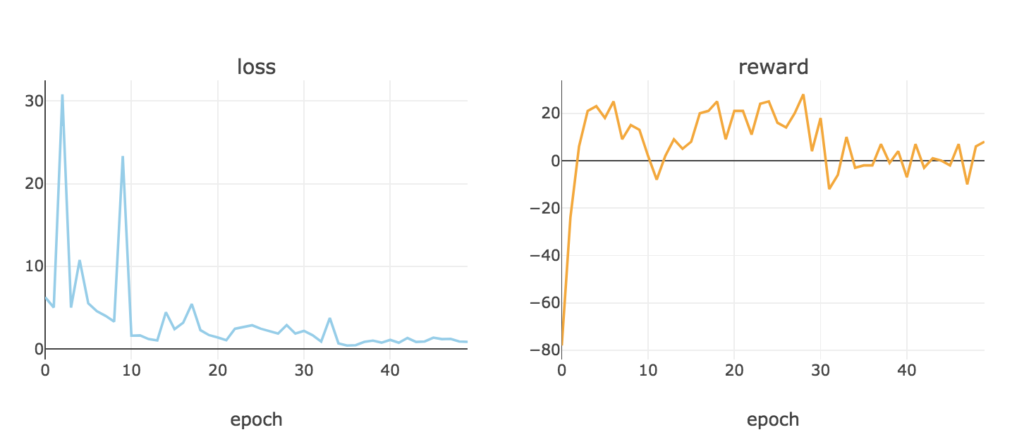
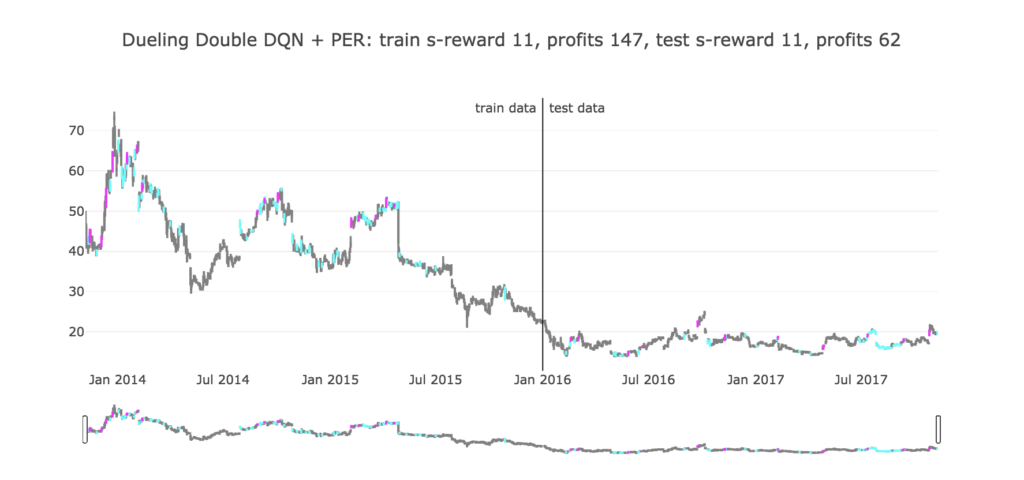
ちゃんと、上がったタイミングを逃さずに売ることが出来ているようです。

やはり全体的に下降しているため、Googleの時と違って、利益は大きくありませんでした。

何か、買いに対しても慎重になっているようで、保持を選択している場面が多いですが、これはどういった条件で買うタイミングを選んでいるのでしょうか。

2. ゴールドマン・サックス

さらにいたずら心で変なデータを学習させてみます。

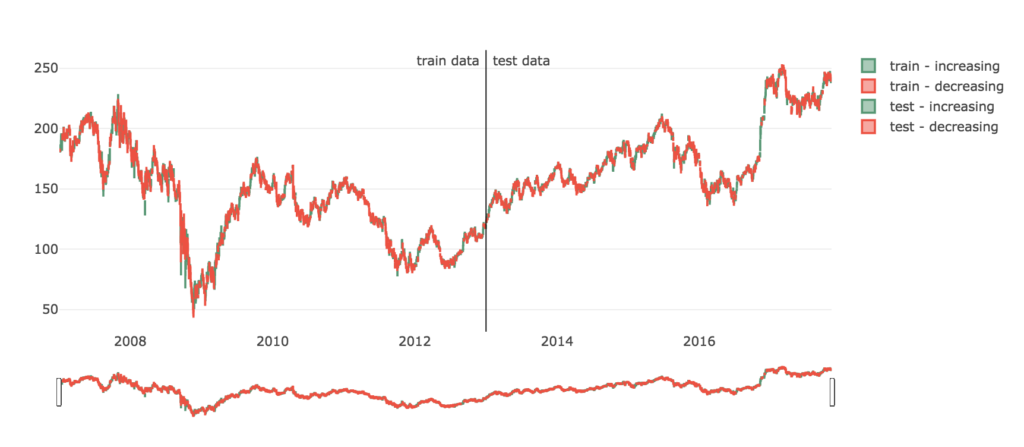
2008年で急激に下降している部分が、いわゆるリーマン・ショックです。

こんな中を何百回もエポックで経験するとなると、逆に学習期間での動きがどのように最適化されるのか、少し興味があります。

学習させてみた結果が以下になります。

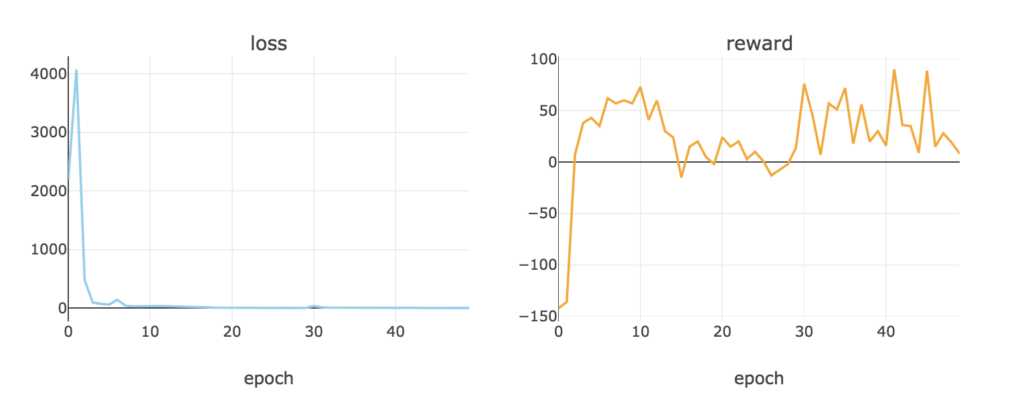
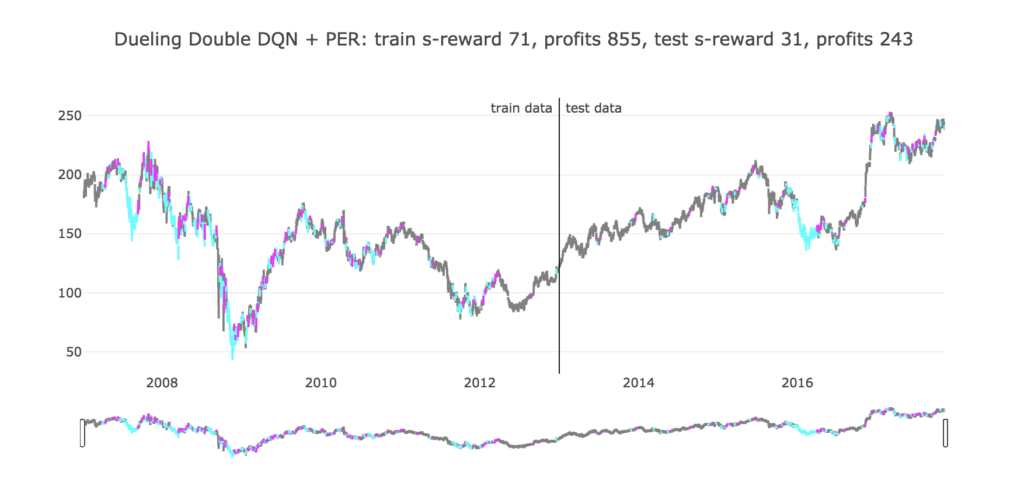
リーマン・ショック中がめちゃくちゃ活発でワロタ。

それでも最終的にはプラスになっているようです。

やはり下がっている最中は買っとけ買っとけになっているようですが、保持を選択するところは、これについてもよく分かりません。

感想

以上、深層強化学習でシステムトレードのエージェントの学習を行ってみました。

前々から一度やってみたかったとは思っていましたが、環境やタスクをよく考えなければならないことを実感しました。

建玉評価額は実際に取引していても見ることが出来ますし、そこで機械的に判断するのは、当然といえば当然ですよね...。

どちらかと言えば、複数の銘柄のデータを食わせて、利益が最大化できるような銘柄の選択の仕方を学習するなどにタスクを置き換えたりした方が良いかもしれません。

また、株価データのみを食わせていましたが、これを会社情報やIR情報などを状態として観測できるようにし、有益な情報を検知して買いや売りを判断させる方が、どちらかと言えば、投資家の人間っぽい行動パターンになるのではないかと思いました。