割と今更ですが、深層学習において、汎化性能を保つための工夫の一つであるDropoutを使って推論を行うことが、近似的にベイズ推論になっているという論文がありますので、それについて記します。
また、実際に試験的にMNIST画像分類で推論をしてみて、様子について確認してみようと思います。
論文の概要
論文は下記になります。
Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning: https://arxiv.org/abs/1506.02142
Dropoutを適用させた深層学習は、deep gaussian modelにおける変分ベイズ推論となる事を理論的に示しています。
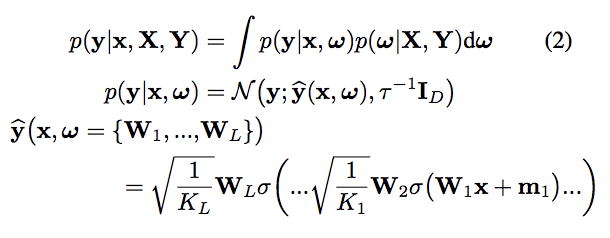
上記の ![]() が事後分布を表しており、これを近似する分布
が事後分布を表しており、これを近似する分布 ![]() を
を
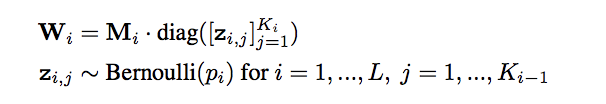
として考え、これがDropoutによってネットワークのユニットをランダムに0にすることと同じことを意味しています。
![]() の予測分布は、以下のようにDropoutを適用したサンプリングの平均を取ることで得ます。
の予測分布は、以下のようにDropoutを適用したサンプリングの平均を取ることで得ます。
論文中では、これを「MC dropout」と呼んでいます。
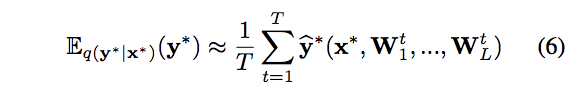
予測分布の不確実性(予測しにくさ)を表す指標として、論文では、分散あるいはエントロピーの利用が提言されており、分散はMC dropoutで、予測分散を計算できることが示されています。
エントロピーも、予測分布から一般的なエントロピーを計算させることができます。
予測分散(論文引用): 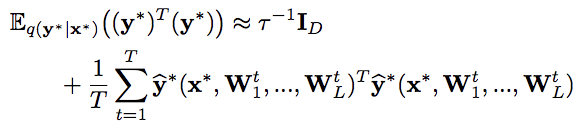
エントロピー(Wikipedia引用): ![]()
MNISTによる実証
実際にDropoutを適用して深層学習モデルを学習し、Dropoutを適用したまま推論を繰り返して、予測分布を作成してみます。
今回は論文と同様に、MNIST画像分類で実験的に行ってみます。
コードは以下にもあげました。
ライブラリはChainerを使いました。
ライブラリをもろもろインポート。
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import chainer
import chainer.functions as F
import chainer.links as L
from chainer.training import extensions
from PIL import Image
from tqdm import tqdm
まずデータを下記のように準備します。
train, valid = chainer.datasets.get_mnist()
train_x, train_y = train._datasets
valid_x, valid_y = valid._datasets
train_x = train_x.reshape(len(train_x), 1, 28, 28).astype(np.float32)
train_y = train_y.astype(np.int32)
valid_x = valid_x.reshape(len(valid_x), 1, 28, 28).astype(np.float32)
valid_y = valid_y.astype(np.int32)
train_dataset = chainer.datasets.tuple_dataset.TupleDataset(train_x, train_y)
valid_dataset = chainer.datasets.tuple_dataset.TupleDataset(valid_x, valid_y)
len(train_dataset), len(valid_dataset)
"""
(60000, 10000)
"""
モデルはちょっとだけ畳み込みも追加して、以下のようなCNNを作りました。
class Model(chainer.Chain):
def __init__(self):
super(Model, self).__init__()
with self.init_scope():
self.conv1 = L.Convolution2D(1, 16, 3)
self.conv2 = L.Convolution2D(16, 32, 3)
self.fc3 = L.Linear(None, 1000)
self.fc4 = L.Linear(1000, 1000)
self.fc5 = L.Linear(1000, 10)
def __call__(self, x, extract_feature=False):
h1 = F.max_pooling_2d(F.relu(self.conv1(x)), 2)
h2 = F.max_pooling_2d(F.relu(self.conv2(h1)), 2)
h3 = F.dropout(F.relu(self.fc3(h2)))
h4 = F.dropout(F.relu(self.fc4(h3)))
y = self.fc5(h4)
return y
学習させます。
gpu = 0
model = L.Classifier(Model())
optimizer = chainer.optimizers.Adam(alpha=1e-4)
optimizer.setup(model)
if gpu >= 0:
chainer.cuda.get_device(gpu).use()
model.to_gpu(gpu)
epoch_num = 10
batch_size = 1000
train_iter = chainer.iterators.SerialIterator(train_dataset, batch_size)
test_iter = chainer.iterators.SerialIterator(valid_dataset, batch_size, repeat=False, shuffle=False)
updater = chainer.training.StandardUpdater(train_iter, optimizer, device=gpu)
trainer = chainer.training.Trainer(updater, (epoch_num, 'epoch'), out='tmp_result')
trainer.extend(extensions.Evaluator(test_iter, model, device=gpu))
trainer.extend(extensions.LogReport(trigger=(1, 'epoch')))
trainer.extend(extensions.LogReport())
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'validation/main/loss', 'main/accuracy', 'validation/main/accuracy', 'elapsed_time']))
trainer.run()

model.to_cpu()
推論させます。
Chainerでは一般的に、chainer.using_config で train 中ではないと設定し、Dropoutを無効にして推定することが多いですが、これを意図的に train 中としてDropoutを有効にします。
上記の概要の通り、1回の推論を行うことで、カテゴリカル分布の観測値を得ることができ、これをサンプリング回数繰り返し推論させることで、「結局どのラベルにどれだけ振り分けられたのか」といった多項分布の観測値を得ることができ、これを平均を取ることで、一枚の画像につき、どのラベルであるかを表す予測分布が得られることになります。
一枚の画像につき推論を繰り返した時に、全てのラベルに均等に振り分けられた場合、全てのラベルの確率が同じである一様分布ができます。
こういった画像は、どのラベルであるか検討がつかないという意味であり、つまり予測しにくい画像ということになります。
逆に予測しやすい画像を推論した結果として得られるサンプリングの分布は、どんなDropoutパターンでも予測ラベルが集中しやすいものになります。
上記の概要にも記した通り、この予測しにくさを定量化するため、今回はそれぞれの画像についてエントロピーを算出してみます。
エントロピーは、確率分布の予測しにくさを表します。
一般的に、確率分布が一様分布に従う時、エントロピーは最大になります。
以下は、バリデーションデータの中から、target_num のラベル番号に絞ってエントロピーを算出し、予測しやすいそのラベルの画像と、予測しにくいそのラベルの画像をプロットするコードを書いてみました。
target_num = 0
sampling_num = 50
target_x = valid_x[np.where(valid_y == target_num)]
entropy = np.zeros((len(target_x)), dtype=np.float32)
for i in tqdm(range(len(target_x))):
x = target_x[i]
x = x[np.newaxis]
preds = np.zeros((sampling_num, 10), dtype=np.float32)
for j in range(sampling_num):
with chainer.using_config('train', True):
preds[j, :] = F.softmax(model.predictor(x), axis=1).data.squeeze()
preds = preds.mean(axis=0)
entropy[i] = np.sum(-preds*np.log(preds))
target_imgs = target_x.reshape(len(target_x), 28, 28)
target_imgs *= 255
target_imgs = target_imgs.astype(np.uint8)
high_entropy_imgs = target_imgs[np.argsort(entropy)[::-1][:30]]
low_entropy_imgs = target_imgs[np.argsort(entropy)[:30]]
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(low_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('low entropy top 30')
plt.show()
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(high_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('high entropy top 30')
plt.show()

予想通りの結果で、うまくいっていそうです。
バリデーションの中から 0 の画像で近似ベイズ推論で得られた予測分布のエントロピーが低かったもののTOP30、高かったもののTOP30を表示してみました。
エントロピーが低いものは予測がしやすい画像になりますので、とても綺麗なお手本のような 0 の画像が集まりました。
逆にエントロピーが高いものは、予測がしにくく、他のラベルと間違えやすい画像ですので、形がいびつであったり、汚い字が集まります。
これを他の数字でも実行してみた結果が以下になります。

1 です。
エントロピーが低いものは、ただ真っ直ぐに線が引かれているだけで、あまり面白くないかもしれないです。
エントロピーが高いものに関しては、字がかすれていたり、あと、線が太すぎても予測を間違えやすい傾向にあるようです。

2 です。
エントロピーが高いものは、かなりひどく、もはや人でも読めなさそうなものも見られます。

3 です。
エントロピーが低いものは、とても綺麗にバランスの取れたお手本のような 3 が集まりました。
エントロピーが高いものは、読めないことは無さそうですが、やはりバランスが悪い字が多いですね。

4 です。
これもエントロピーが低いものは、バランスが良いです。

5 です。
これも綺麗な 5 が集まっています。
エントロピーが高いものは、汚いものだらけです。

6 です。
6 に関しては、バランス的には少し傾いてしまった方が、深層学習は間違えにくい傾向にあるようです。
エントロピーが高いものは酷いですね。

7 です。
エントロピーが高いものは、もうかなり汚く、これも人が読んでも間違えそうなものが多いです。

8 です。
こちらもエントロピーが低いものは、バランスの良い 8 が集まっています。
エントロピーが高いものは、片方の丸が潰れていたり、切れすぎて丸になっていないようなものが集まってきました。

9 です。
エントロピーが低いものは、正しい書き順で書かれたものが集まっている印象で、エントロピーが高いものは、6を逆順にしたような書き方をしたものが集まってきました。
感想
Dropoutによる近似ベイズ推論について記しました。
Dropoutを入れるだけなので、様々な深層学習のネットワークアーキテクチャに適用することができ、結果も見ていて面白いです。
実際にオブジェクト検出のモデルにおいて、これを使った例として、以下のような論文も出ています。
Dropout Sampling for Robust Object Detection in Open-Set Conditions: https://arxiv.org/abs/1710.06677
また、1つの入力につきサンプリング回数だけ推論を繰り返すことになるため、予測には少し計算に時間がかかります。
それに、とりあえず予測がしにくいというデータは教えてくれますが、なぜ予測しにくいのか、どうすれば間違えにくくなるのかといった点は、やはり結果を見て自分で考察していく必要はありそうです。
追記(2018-07-25)
ちょっとした興味本位のテストを試してみました。

コメント