株やります←
株価取引において、最近では「スイングトレード」などというワードを見るようになり、下記のような書籍も書店に並ぶようになりました。
ちなみに上記書籍は私も買いました←
ただ、こういった取引方法は、企業の業績だったり将来性だったりといった、いわゆるファンダメンタルズ分析を行わず、テクニカル分析を中心に取引を行うらしいです。
そのように聞くと個人的に気になるのは、「テクニカル分析って本当に効果があるのか？」というところです。
なので、実際にテクニカル分析でよく使われている指標をPythonで実装してみて、過去の株価推移のデータで効果について調べてみました。
ちなみに私は金融素人なので、専門家から見れば、とんちんかんなことをやっている可能性ありです。
使用するデータ
データは以下のサイトからダウンロードできるものを使用します。
2017年の全銘柄の日足株価データです。
- http://www.geocities.co.jp/WallStreet-Stock/9256/data2017.htm
これらのデータにテクニカル指標を使った分析を行ってみて、結果を評価してみます。
今回使うライブラリをもろもろインポート。
import glob
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pylab as plt
from scipy import stats
from tqdm import tqdm
ダウンロードしたデータから、銘柄コードだけ取得。
paths = glob.glob('path/to/Downloads/2017/*.txt')
col_names = ['code', 'name', 'open', 'high', 'low', 'close', 'volume']
df_code = pd.read_csv(paths[0], delimiter='\t', encoding='SHIFT-JIS', header=None, names=col_names)
codes = df_code.iloc[1:, 0].as_matrix()
for path in tqdm(paths[1:]):
df_code = pd.read_csv(path, delimiter='\t', encoding='SHIFT-JIS', header=None, names=col_names)
codes = list(set(codes) & set(df_code.iloc[1:, 0].as_matrix()))
len(codes)
"""
3008
"""
銘柄コードの規則はよくわかりませんが、今回は企業の銘柄コードのみで評価してみたかったので、対象コードを絞ります。
目視で確認したところ、1700より大きいコードであれば、企業の銘柄コードとなりそうでした。
codes = np.array(codes)[np.array(codes) > 1700]
len(codes)
"""
2898
"""
これについて、2017年のうちはすべての日付で存在していた銘柄コードの株価のみ取得しデータフレーム化しました。
df_all = pd.read_csv(paths[0], delimiter='\t', encoding='SHIFT-JIS', header=None, names=col_names)
date = str(df_all.iloc[0, 0])
date = date[:4] + '-' + date[4:6] + '-' + date[6:]
df_all['date'] = date
df_all = df_all.iloc[1:, :]
df_all = df_all[df_all['code'].isin(codes)]
for path in tqdm(paths[1:]):
df = pd.read_csv(path, delimiter='\t', encoding='SHIFT-JIS', header=None, names=col_names)
date = str(df.iloc[0, 0])
date = date[:4] + '-' + date[4:6] + '-' + date[6:]
df['date'] = date
df = df.iloc[1:, :]
df = df[df['code'].isin(codes)]
df_all = pd.concat([df_all, df])
df_all['date'] = pd.to_datetime(df_all['date'])
df_all = df_all.sort_values(by=['code', 'date'], ascending=True)
len(df_all)
"""
715806
"""
テクニカル分析の指標の実装
まずはテクニカル分析で使われる指標について、Pythonで実装してみます。
参考に銘柄コードを1つに決め、期間も１年は長いので、半年程度に切ります。
銘柄はトヨタ（7203）、対象期間は2017年前半（2017-01-01〜2017-06-30）としました。
c = 7203
start_date = '2017-01-01'
end_date = '2017-06-30'
ローソク足
買いポジションを判断する指標かどうかはさておき、ローソク足もテクニカル分析の指標の1つのようです。
これに関しては説明は不要ですね。
Pythonでは、matplotlibでローソク足をプロットできます。
# ローソク足
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
fig, ax = plt.subplots(figsize=(10, 5))
matplotlib.finance.candlestick2_ohlc(
ax,
opens=df_tmp['open'],
highs=df_tmp['high'],
lows=df_tmp['low'],
closes=df_tmp['close'],
width=1.0,
colorup='green',
colordown='red',
)
plt.show()
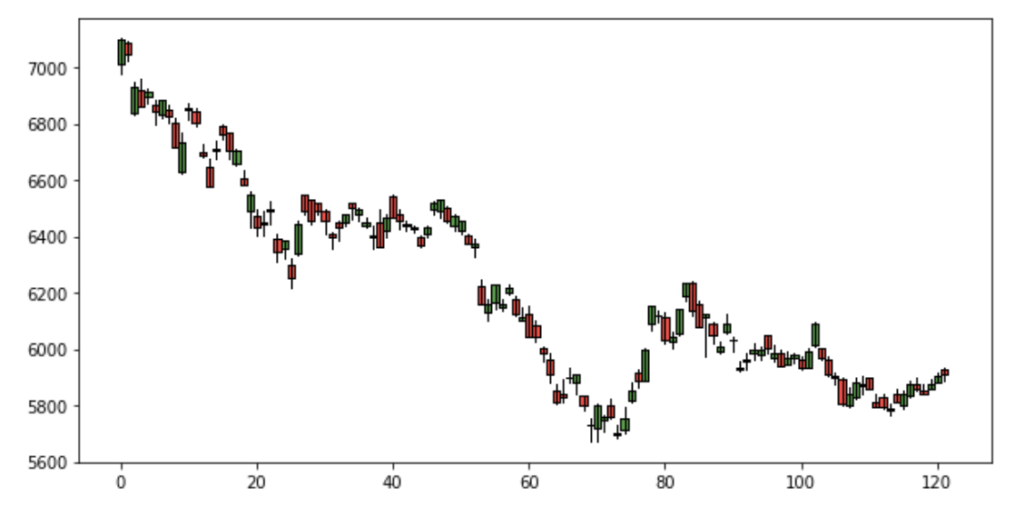
matplotlibdはもちろん、大概のプロット系のライブラリには、ローソク足のプロット機能がついていることが多いですね。
以前に書いた記事で、深層強化学習で為替取引みたいなことをやらせた時にもローソク足をプロットしていて、この時はPlotlyというライブラリを使いました。
http://www.ie110704.net/2018/02/24/%E6%B7%B1%E5%B1%A4%E5%BC%B7%E5%8C%96%E5%AD%A6%E7%BF%92%E3%81%A7%E3%82%B7%E3%82%B9%E3%83%86%E3%83%A0%E3%83%88%E3%83%AC%E3%83%BC%E3%83%89%E3%81%97%E3%81%A6%E3%81%BF%E3%81%9F%E3%81%8B%E3%81%A3%E3%81%9F/
ちなみにこのローソク足ですが、今では世界中で使われている指標ではありますが、実は日本産であり、江戸時代に初めて考案されたものらしいです。
移動平均線
移動平均は、直近の 
個のデータに対する単純な平均です。
例えば、 日期間の終値の移動平均は、終値 
について、
となります。
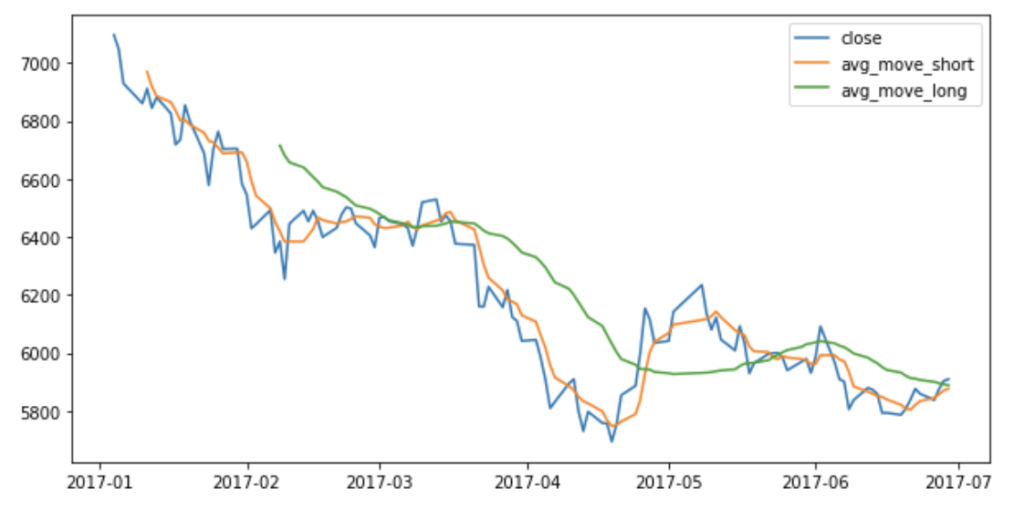
また、期間が異なる移動平均線を組み合わせることにより、買い・売りのシグナルを判断することができます。
期間の短い移動平均線が、期間の長い移動平均線を上に超えると、ゴールデンクロスと呼ばれ、買いシグナルと判断できます。
逆に、期間の短い移動平均線が、期間の長い移動平均線を下に抜けるとデッドクロスと呼ばれ、売りシグナルと判断できます。
# 移動平均線（Moving Average; MA）
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
ma_short_period = 5
ma_long_period = 25
avg_move_short = df_tmp['close'].rolling(ma_short_period).mean().values
avg_move_long = df_tmp['close'].rolling(ma_long_period).mean().values
cross = avg_move_short > avg_move_long
golden = np.array((cross != np.roll(cross, 1)) & (cross == True))
dead = np.array((cross != np.roll(cross, 1)) & (cross == False))
plt.figure(figsize=(10, 5))
plt.plot(df_tmp['date'], df_tmp['close'])
plt.plot(df_tmp['date'], avg_move_short, label='avg_move_short')
plt.plot(df_tmp['date'], avg_move_long, label='avg_move_long')
plt.legend()
plt.show()
golden, dead
ボリンジャーバンド
ボリンジャーバンドは、移動平均線に標準偏差を取り入れたものです。
均衡状態の株価が正規分布に従っていることを仮定とし、標準偏差の考え方によれば、
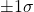内に株価が含まれる確率は 68.3%
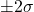内に株価が含まれる確率は 95.5%
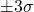内に株価が含まれる確率は 99.7%
と見ることができます。
例えば、 より外にレートがあるときに逆のポジションを取れば、95.5%の確率で内側に戻ってくるとも考えられますし、あるいは、株価が均衡状態でなくなったと判断することもできます。
# ボリンジャーバンド
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
period = 25
avg_move = df_tmp['close'].rolling(period).mean().values
sigma = df_tmp['close'].rolling(period).std(ddof=0).values
sigma_plus1 = avg_move+sigma
sigma_plus2 = avg_move+sigma*2
sigma_plus3 = avg_move+sigma*3
sigma_minus1 = avg_move-sigma
sigma_minus2 = avg_move-sigma*2
sigma_minus3 = avg_move-sigma*3
plt.figure(figsize=(10, 5))
plt.plot(df_tmp['date'], df_tmp['close'])
plt.plot(df_tmp['date'], avg_move, label='avg_move')
plt.plot(df_tmp['date'], sigma_plus1, label='sigma_plus1')
plt.plot(df_tmp['date'], sigma_plus2, label='sigma_plus2')
plt.plot(df_tmp['date'], sigma_plus3, label='sigma_plus3')
plt.plot(df_tmp['date'], sigma_minus1, label='sigma_minus1')
plt.plot(df_tmp['date'], sigma_minus2, label='sigma_minus2')
plt.plot(df_tmp['date'], sigma_minus3, label='sigma_minus3')
plt.legend(loc=2)
plt.show()
np.array(df_tmp['close'] > sigma_plus2), np.array(df_tmp['close'] < sigma_minus2)
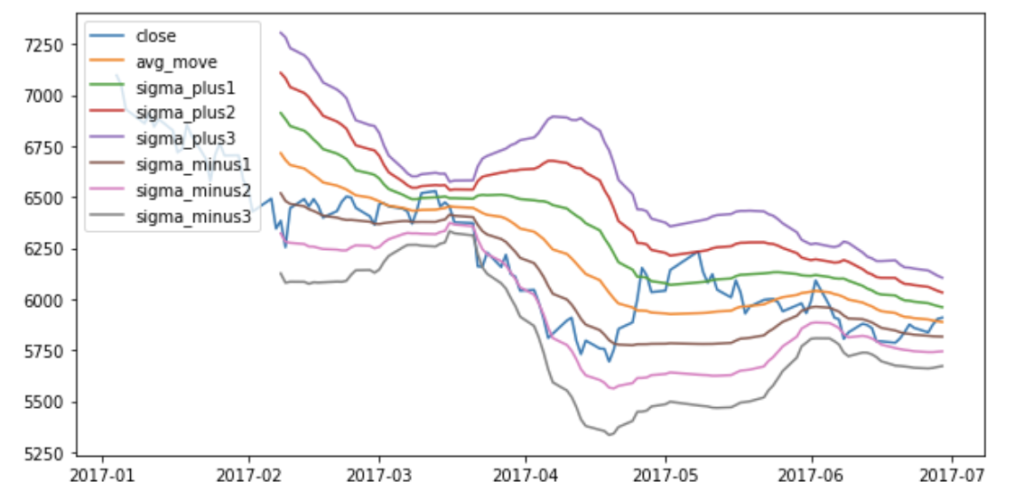
トヨタの株価は、この期間のデータはちょっと全体的に帯が広くなっていますね。
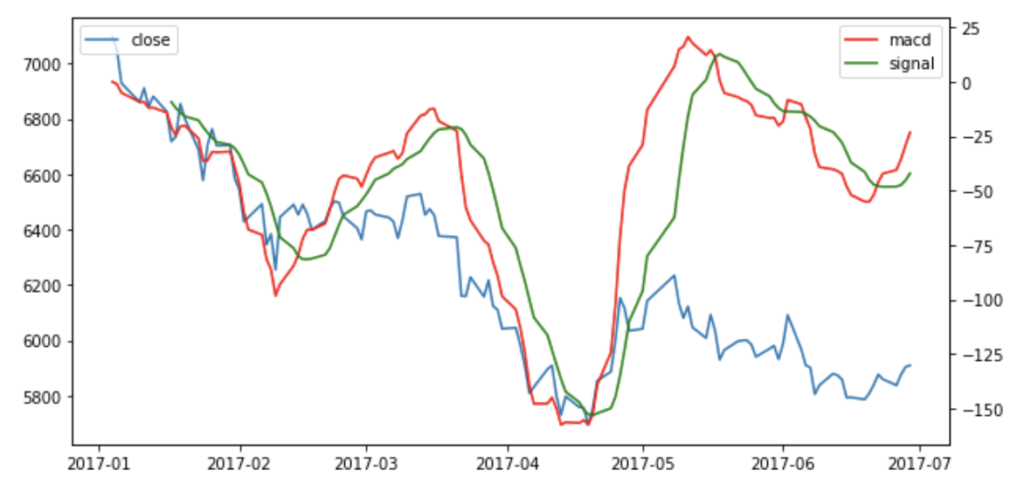
移動平均収束拡散法（Moving Average Convergence/Divergence; MACD）
移動平均線は、単純に一定期間のすべての株価を平等に平均を取っていましたが、ここでは、より直近の新しい株価の方が影響力が高いという考え方から、直近の株価の重みを優先するように移動平均を計算しています。
これを指数平滑移動平均（Exponential Moving Average; EMA）と呼び、直近から遠くなるほど、指数関数的に重みを減少させていきます。
そして、この移動平均を２つ組み合わせて、MACD（マックディー）とシグナルを計算します。
具体的には、
- MACD ＝ 短期平均 - 長期平均
- シグナル ＝ MACDの単純移動平均線
です。
MACDがシグナルを上に抜けるとゴールデンクロスで買いシグナル、下に抜けるとデッドクロスで売りシグナルと判断できます。
# 移動平均収束拡散法（Moving Average Convergence/Divergence; MACD）
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
ema_short_period = 12
ema_long_period = 26
sma_period = 9
macd = df_tmp['close'].ewm(span=ema_short_period).mean() - df_tmp['close'].ewm(span=ema_long_period).mean()
signal = macd.rolling(sma_period).mean()
cross = macd > signal
golden = np.array((cross != np.roll(cross, 1)) & (cross == True))
dead = np.array((cross != np.roll(cross, 1)) & (cross == False))
fig, ax1 = plt.subplots(figsize=(10, 5))
ax1.plot(df_tmp['date'], df_tmp['close'])
ax1.legend(loc=2)
ax2 = ax1.twinx()
ax2.plot(df_tmp['date'], macd, color='red', label='macd')
ax2.plot(df_tmp['date'], signal, color='green', label='signal')
ax2.legend(loc=1)
plt.show()
golden, dead
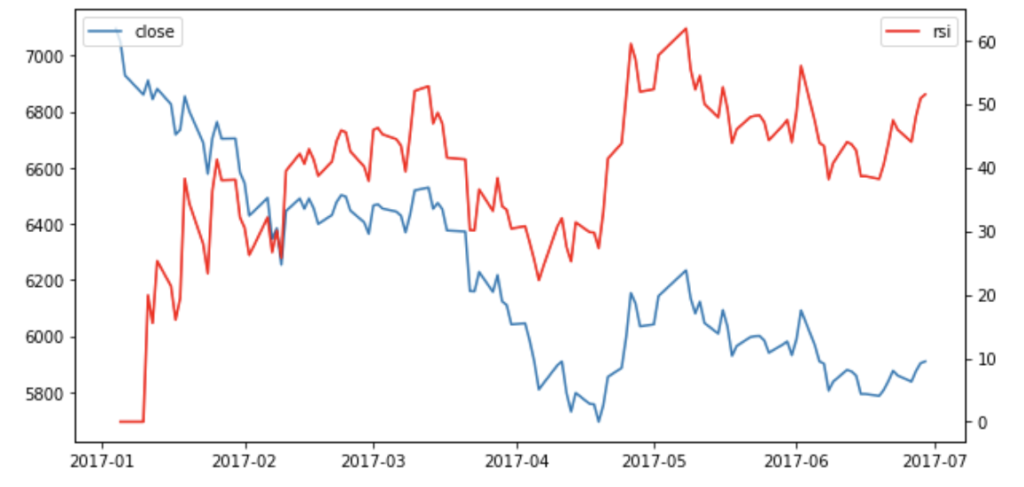
相対力指数（Relative Strength Index; RSI）
RSIは、一定期間の株価の変動に対して、どのくらい上昇しているのかを見極める指標です。
一定期間において、「上昇した日の値幅合計」と「下落した日の値幅合計」を合わせたもののうち、前者の比率を表します。
これに相場の過熱感（買われすぎ、売られすぎ）を判断します。
一般的に、RSIが、
- 70％～100％：買いが優勢 → 上昇トレンド → 買われすぎ
- 50％：中立
- 0％～30％： 売りが優勢 →下落トレンド → 売られすぎ
と判断するようです。
RSIが買われすぎゾーンに入った時は売りシグナル、売れらすぎゾーンに入った時は買いシグナルとなります。
# RSI
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
rsi_period = 14
diff = df_tmp['close'].diff(1)
positive = diff.clip_lower(0).ewm(alpha=1/rsi_period).mean()
negative = diff.clip_upper(0).ewm(alpha=1/rsi_period).mean()
rsi = 100-100/(1-positive/negative)
fig, ax1 = plt.subplots(figsize=(10, 5))
ax1.plot(df_tmp['date'], df_tmp['close'])
ax1.legend(loc=2)
ax2 = ax1.twinx()
ax2.plot(df_tmp['date'], rsi, color='red', label='rsi')
ax2.legend(loc=1)
plt.show()
np.array(rsi < 20), np.array(rsi > 80)
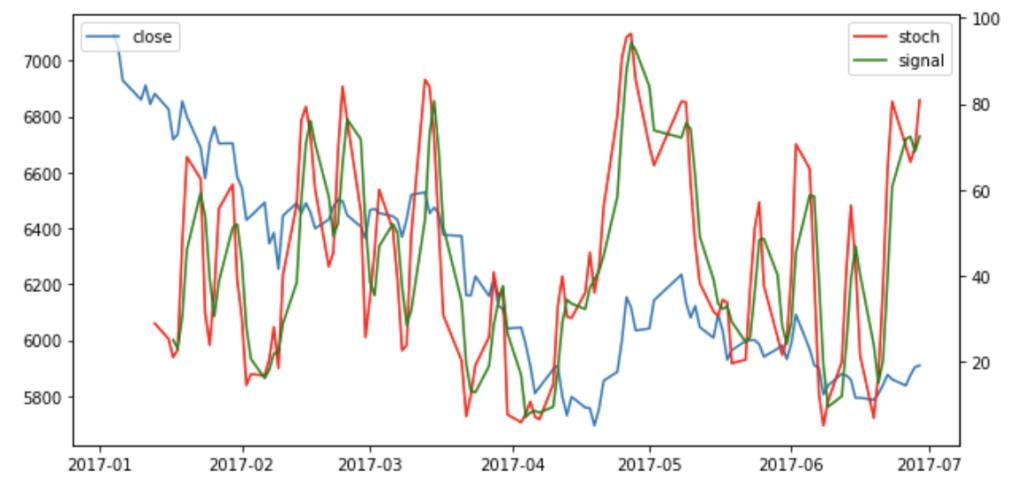
ストキャスティクス
「％K」と「％D」の2本のラインを利用したファーストストキャスティックスと、「Slow％K」と「Slow％D」の2本の線を利用したスローストキャスティクスという、2種類の活用歩法があります。
通常は、スローストキャスティクスの方が実用的なようですので、今回はそちらによるシグナル取得を実装しました。
ファーストストキャスティックス
- ％K ＝（直近の終値－過去5日間の最安値）÷（過去5日間の最高値－過去5日間の最安値）× 100
- ％D = 3日間の％Kの単純移動平均
スローストキャスティクス
- Slow％K= %D
- Slow％D= 3日間の％Dの単純移動平均
であり、「Slow％D」が0～20％で「Slow％K」が「Slow％D」を上抜け（ゴールデンクロス）で強い買いシグナルと見ます。
# ストキャスティクス（Stochastics）
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
k_period = 5
d_period = 3
slowing_period = 3
hline = df_tmp['high'].rolling(k_period).max()
lline = df_tmp['low'].rolling(k_period).min()
sumlow = (df_tmp['close']-lline).rolling(slowing_period).sum()
sumhigh = (hline-lline).rolling(slowing_period).sum()
stoch = sumlow/sumhigh*100
signal = stoch.rolling(d_period).mean()
cross = stoch > signal
golden = np.array((cross != np.roll(cross, 1)) & (cross == True) & (stoch < 20) & (signal < 20))
dead = np.array((cross != np.roll(cross, 1)) & (cross == False) & (stoch > 80) & (signal > 80))
fig, ax1 = plt.subplots(figsize=(10, 5))
ax1.plot(df_tmp['date'], df_tmp['close'])
ax1.legend(loc=2)
ax2 = ax1.twinx()
ax2.plot(df_tmp['date'], stoch, color='red', label='stoch')
ax2.plot(df_tmp['date'], signal, color='green', label='signal')
ax2.legend(loc=1)
plt.show()
golden, dead
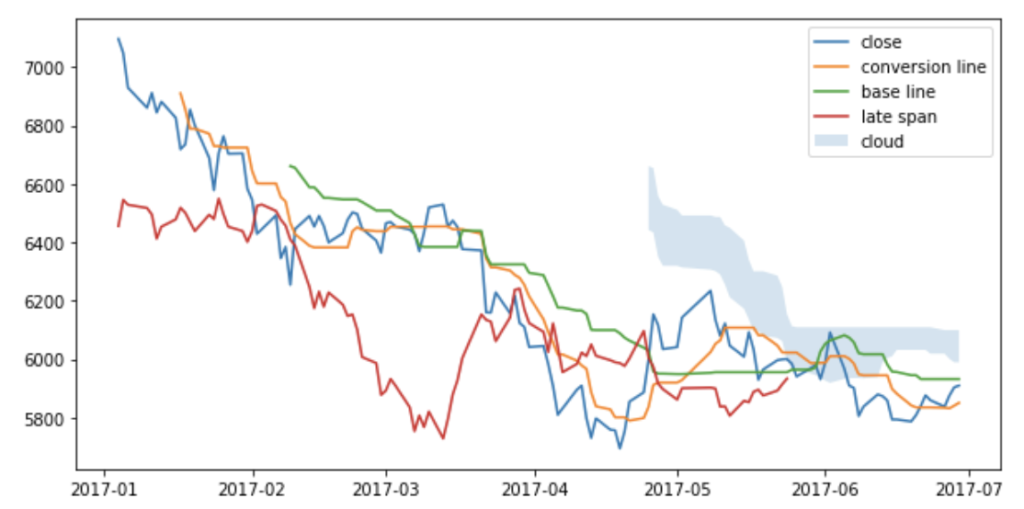
一目均衡表
最後に、一目均衡表というものを紹介します。
この一目均衡表も、ローソク足と同様国産のテクニカル指標で、世界中で利用されているものらしいです。
ゴールデンクロス・デッドクロスと同様、転換線（conversion_line）と基準線（base_line）が交差する部分がトレンドの変換点であり、転換線が基準線を上抜けたら好転、下抜けたら逆転とみなします。
また、転換線と基準線、最高値と最安値を使った先行スパンと呼ばれる線で雲を描き、また、終値を使って遅延スパンという線も描いて、この両方をローソク足が上抜けた時にシグナルと判断するようです。
しかしこれは、勉強不足でよく分からないのですが、その日時点において分かるのは26日前のシグナルであり、これまでの指標と違って、当日にシグナルを得られない指標のように思うのですが、どうでしょうか。
上記を含め、今回はいまいち使い方が理解できませんでしたので、今回はこの指標は使っての効果測定は実施しませんでした。
# 一目均衡表
df_tmp = df_all[df_all['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
conversion_line_period = 9
base_line_period = 26
span_period = 52
conversion_line = (df_tmp['high'].rolling(window=conversion_line_period).max() + df_tmp['low'].rolling(window=conversion_line_period).min())/2
base_line = (df_tmp['high'].rolling(window=base_line_period).max() + df_tmp['low'].rolling(window=base_line_period).min())/2
leading_span1 = ((conversion_line + base_line)/2)[:-base_line_period]
leading_span2 = ((df_tmp['high'].rolling(window=span_period).max() + df_tmp['low'].rolling(window=span_period).min())/2)[:-base_line_period]
late_span = df_tmp['high'][base_line_period:]
plt.figure(figsize=(10, 5))
plt.plot(df_tmp['date'], df_tmp['close'])
plt.plot(df_tmp['date'], conversion_line, label='conversion line')
plt.plot(df_tmp['date'], base_line, label='base line')
plt.fill_between(df_tmp['date'][base_line_period:].as_matrix(), leading_span1, leading_span2, alpha=0.2, label='cloud')
plt.plot(df_tmp['date'][:-base_line_period].as_matrix(), late_span, label='late span')
plt.legend()
plt.show()
テクニカル指標の買いシグナルからの株価推移
さて、テクニカル指標をいくつか実装できたところで、実際にテクニカル指標が買いシグナルと判断した時に、その後の株価の推移がちゃんと上がっていくのかどうかを見ていきたいと思います。
各指標による買いシグナルの取得を関数化
今回は売りシグナルについては無視するとし、各テクニカル指標で買いシグナルを取得する関数を定義しておきます。
各指標において、次のような条件を満たした時に買いシグナルと判断することにします。
- MA: ゴールデンクロス
- ボリンジャーバンド: 株価が
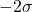を下抜けた時 - MACD: ゴールデンクロス
- RSI: RSIが20%を下回った時
- ストキャスティクス: Slow％Dが20％を下回っていて、Slow％KがSlow％Dをゴールデンクロス
実装したコードが以下。
# MAのゴールデンクロスによる買いシグナルの取得
def get_buy_signals_ma(df, ma_short_period=5, ma_long_period=25):
avg_move_short = df['close'].rolling(ma_short_period).mean().values
avg_move_long = df['close'].rolling(ma_long_period).mean().values
cross = avg_move_short > avg_move_long
golden = np.array((cross != np.roll(cross, 1)) & (cross == True))
return golden
# ボリンジャーバンドの-2σによる買いシグナルの取得
def get_buy_signals_bollinger(df, bollinger_period=25):
avg_move = df['close'].rolling(bollinger_period).mean().values
sigma = df['close'].rolling(bollinger_period).std(ddof=0).values
sigma_minus2 = avg_move-sigma*2
buy_signals = np.array(df['close'] < sigma_minus2)
return buy_signals
# MACDのゴールデンクロスによる買いシグナルの取得
def get_buy_signals_macd(df, ema_short_period=12, ema_long_period=26, sma_period=9):
macd = df['close'].ewm(span=ema_short_period).mean() - df['close'].ewm(span=ema_long_period).mean()
signal = macd.rolling(sma_period).mean()
cross = macd > signal
golden = np.array((cross != np.roll(cross, 1)) & (cross == True))
return golden
# RSIによる買いシグナルの取得
def get_buy_signals_rsi(df, rsi_period=14, rsi_thresold=20):
diff = df['close'].diff(1)
positive = diff.clip_lower(0).ewm(alpha=1/rsi_period).mean()
negative = diff.clip_upper(0).ewm(alpha=1/rsi_period).mean()
rsi = 100-100/(1-positive/negative)
buy_signals = np.array(rsi < rsi_thresold)
return buy_signals
# ストキャスティクスのゴールデンクロスによる買いシグナルの取得
def get_buy_signals_stochastics(df, k_period=5, d_period=3, slowing_period=3):
hline = df['high'].rolling(k_period).max()
lline = df['low'].rolling(k_period).min()
sumlow = (df['close']-lline).rolling(slowing_period).sum()
sumhigh = (hline-lline).rolling(slowing_period).sum()
stoch = sumlow/sumhigh*100
signal = stoch.rolling(d_period).mean()
cross = stoch > signal
golden = np.array((cross != np.roll(cross, 1)) & (cross == True) & (stoch < 20) & (signal < 20))
return golden
ブートストラップ法による信頼区間
いくつかの銘柄について、上記のような買いシグナル時点からの株価がどのように推移したかについてプロットしてみたいと思います。
しかし、例えば平均値を取るとしても、全銘柄に対して平均してしまうと大きな外れ値に引きずられてしまい、うまく評価できません。
ここは、未来の株価の推移についても母集団として含めると仮定して、いくつかの銘柄をサンプリングすることにします。
また、銘柄を選択した時に遭遇するであろう株価推移という観点から、平均値だけでなく、中央値もプロットしてみたいです。
さらに、これらについて点推定だけでなく、信頼区間も出してみたいので、今回はブートストラップ信頼区間を算出することにしてみました。
def calc_bootstrap_ci(data, bootstrap_num=1000, stat='mean'):
stats = np.zeros((bootstrap_num), dtype=np.float32)
for i in range(bootstrap_num):
sample = np.random.choice(data, size=len(data))
if stat == 'mean':
stats[i] = np.mean(sample)
elif stat == 'median':
stats[i] = np.median(sample)
mean = np.mean(stats)
sd = np.std(stats)
ci = (mean-1.96*sd, mean+1.96*sd)
return mean, ci
ブートストラップ法は、1回の標本調査で得られたサンプルデータから、復元抽出を許して同じ標本数を取得するということを繰り返すことで、標本調査を何回も行ったサンプルデータを得るとみなす方法の総称です。
サンプルデータが極限的に母集団の性質を表すことを利用しています。
これにより、各ループで得られたサンプルデータに対する統計量が多数得られることになりますので、これについて、平均値と標準誤差を計算することで、関心のある信頼区間を計算することができます。
株価推移および株価統計量のブートストラップ信頼区間のプロット関数化
以降は、買いシグナル取得の関数を変えて、それぞれ信頼区間をプロットするという、同じ流れになりますので、全部関数化しちゃいます。
以下がコード。
# 各株価の推移
def plot_holding_period_prices(df, start_date, end_date, codes, sampling_num, holding_period, get_buy_signals_method):
target_codes = np.random.choice(codes, size=sampling_num)
target_codes_prices = np.empty((holding_period+1, 1), dtype=np.float32)
plt.figure(figsize=(9, 3))
for c in tqdm(target_codes):
df_tmp = df[df['code'] == c]
df_tmp = df_tmp[(start_date < df_tmp['date']) & (df_tmp['date'] < end_date)]
buy_signals = get_buy_signals_method(df_tmp)
base_closes = df_tmp['close'][buy_signals].as_matrix()
prices = np.zeros((holding_period+1, len(base_closes)), dtype=np.float32)
for d in range(holding_period+1):
prices[d, :] = df_tmp['close'][np.roll(buy_signals, d)].as_matrix()/base_closes*100
for r in prices.transpose():
plt.plot(list(range(holding_period+1)), r, color='black', alpha=0.2)
target_codes_prices = np.hstack((target_codes_prices, prices))
plt.plot(list(range(holding_period+1)), [100]*(holding_period+1), color='r')
plt.xticks(list(range(holding_period+1)))
plt.xlim(0, holding_period)
plt.ylim(80, 120)
plt.xlabel('holding period')
plt.ylabel('stock price (ratio)')
plt.grid()
plt.show()
return target_codes_prices
# 各保有時点での株価の平均値/中央値とブートストラップ信頼区間
def plot_bootstrap_ci(target_codes_prices, holding_period, stat):
prices_stat = np.zeros((holding_period+1), dtype=np.float32)
prices_stat_ci_lower = np.zeros((holding_period+1), dtype=np.float32)
prices_stat_ci_upper = np.zeros((holding_period+1), dtype=np.float32)
for i, p in enumerate(target_codes_prices):
s, ci = calc_bootstrap_ci(p, stat=stat)
prices_stat[i] = s
prices_stat_ci_lower[i] = ci[0]
prices_stat_ci_upper[i] = ci[1]
plt.figure(figsize=(9, 3))
plt.plot(list(range(holding_period+1)), [100]*(holding_period+1), color='r')
plt.plot(list(range(holding_period+1)), prices_stat, color='black', label=stat)
plt.fill_between(list(range(holding_period+1)), prices_stat_ci_lower, prices_stat_ci_upper, color='black', alpha=0.2, label='confidence iterval')
plt.xticks(list(range(holding_period+1)))
plt.xlim(0, holding_period)
plt.ylim(80, 120)
plt.xlabel('holding period')
plt.ylabel('stock price (ratio)')
plt.legend()
plt.grid()
plt.show()
移動平均線
それでは、検証してみます。
買いシグナルから何日間株価の動きを見るのかは20日間とし、買いシグナルを探す株価コードはランダムに100件取ってくることにしました。
sampling_num = 100
holding_period = 20
それではまず移動平均線のゴールデンクロスからの株価推移のプロット。
# MAの買いシグナルからの株価推移
# 各株価の推移
target_codes_prices = plot_holding_period_prices(
df=df_all,
start_date=start_date,
end_date=end_date,
codes=codes,
sampling_num=sampling_num,
holding_period=holding_period,
get_buy_signals_method=get_buy_signals_ma
)
# 各保有時点での株価の平均値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='mean')
# 各保有時点での株価の中央値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='median')
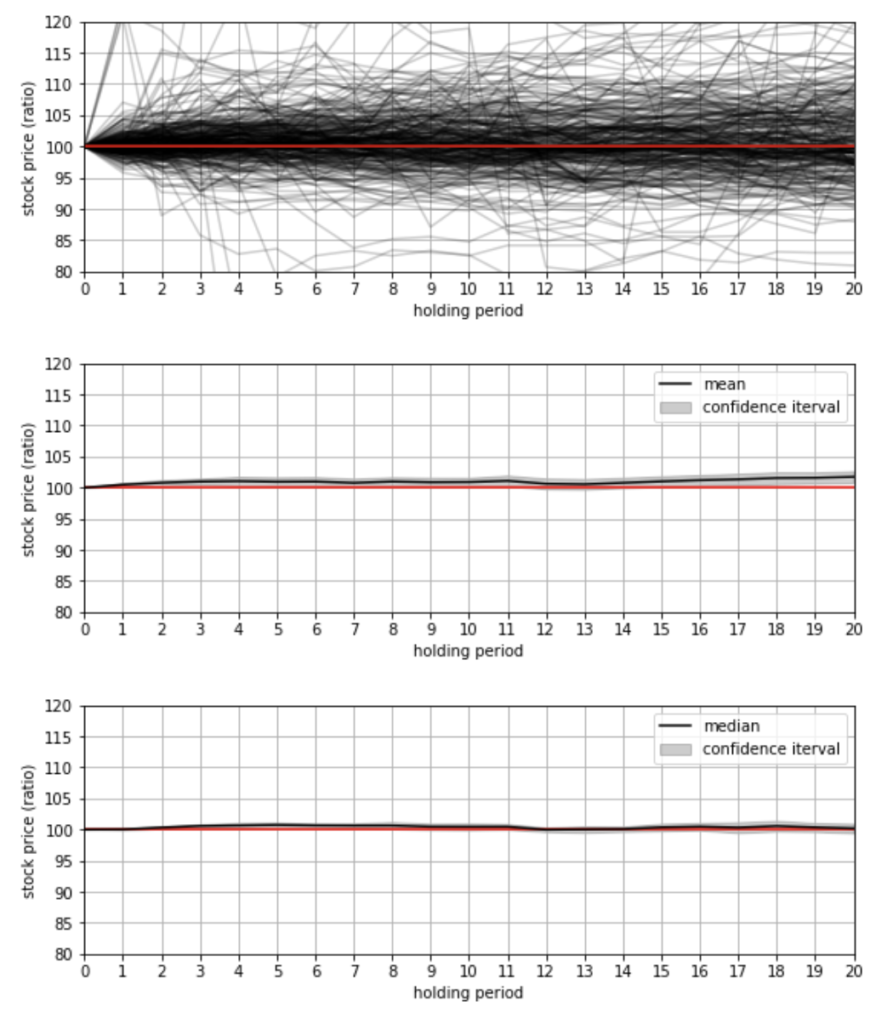
3つのグラフのうち、1つ目のグラフは、選んできた100銘柄について、買いシグナルが発生した時の株価を100%とした後の株価の推移を時系列で表したものです。
80%〜120%を表示範囲としましたが、はるかにそれらを突き抜けているようなパターンもいくつかあります。
株価は怖いですね。
2つ目、3つ目はそれぞれ、平均値、中央値とそのブートストラップ信頼区間を表しています。
うーん、いまいち見づらいですけど、こうしてみると、やはり平均は外れ値に引っ張られているのでしょうか。
中央値で見るとあまり変わらなそうなことが分かります。
ボリンジャーバンド
続いて、ボリンジャーバンドの買いシグナルからの株価推移。
# ボリンジャーバンドの買いシグナルからの株価推移
# 各株価の推移
target_codes_prices = plot_holding_period_prices(
df=df_all,
start_date=start_date,
end_date=end_date,
codes=codes,
sampling_num=sampling_num,
holding_period=holding_period,
get_buy_signals_method=get_buy_signals_bollinger
)
# 各保有時点での株価の平均値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='mean')
# 各保有時点での株価の中央値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='median')
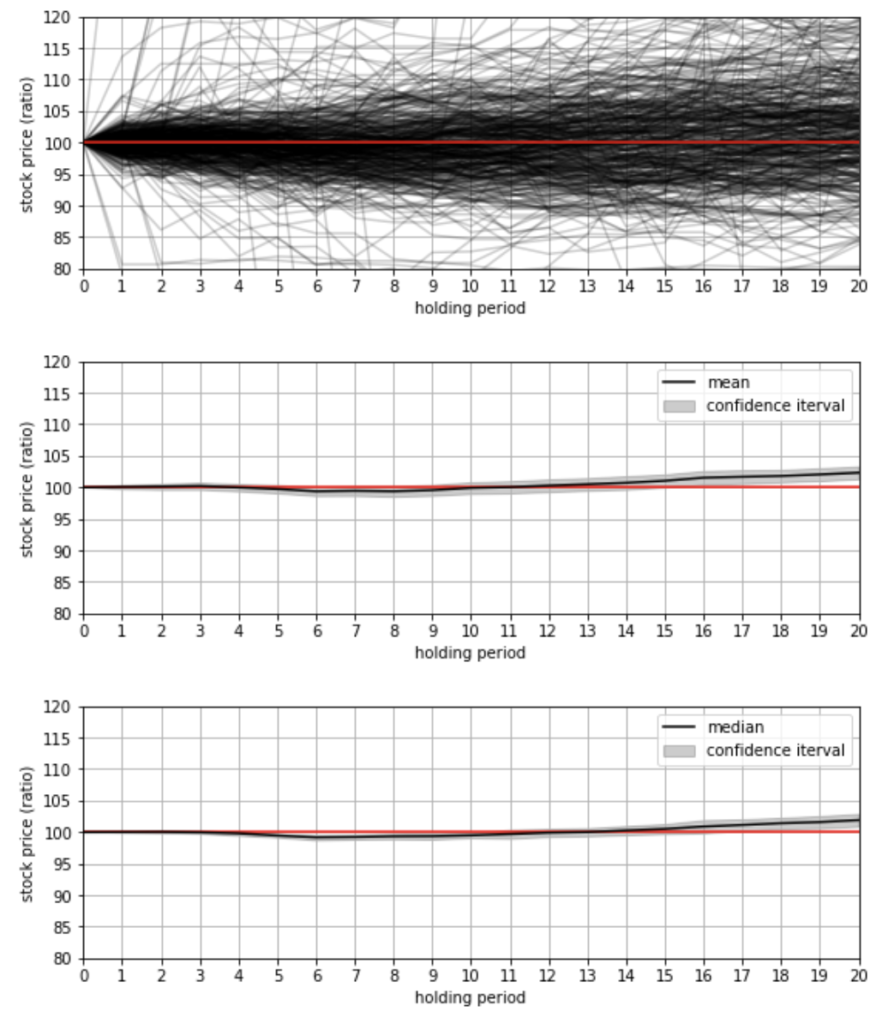
こちらもあまり変わりはなさそうですが、中央値の方も、保有日数15日目以降になると、緩やかに上がってきているようです。
移動平均収束拡散法
MASDの買いシグナルからの株価推移。
# MACDのゴールデンクロスからの株価推移
# 各株価の推移
target_codes_prices = plot_holding_period_prices(
df=df_all,
start_date=start_date,
end_date=end_date,
codes=codes,
sampling_num=sampling_num,
holding_period=holding_period,
get_buy_signals_method=get_buy_signals_macd
)
# 各保有時点での株価の平均値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='mean')
# 各保有時点での株価の中央値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='median')
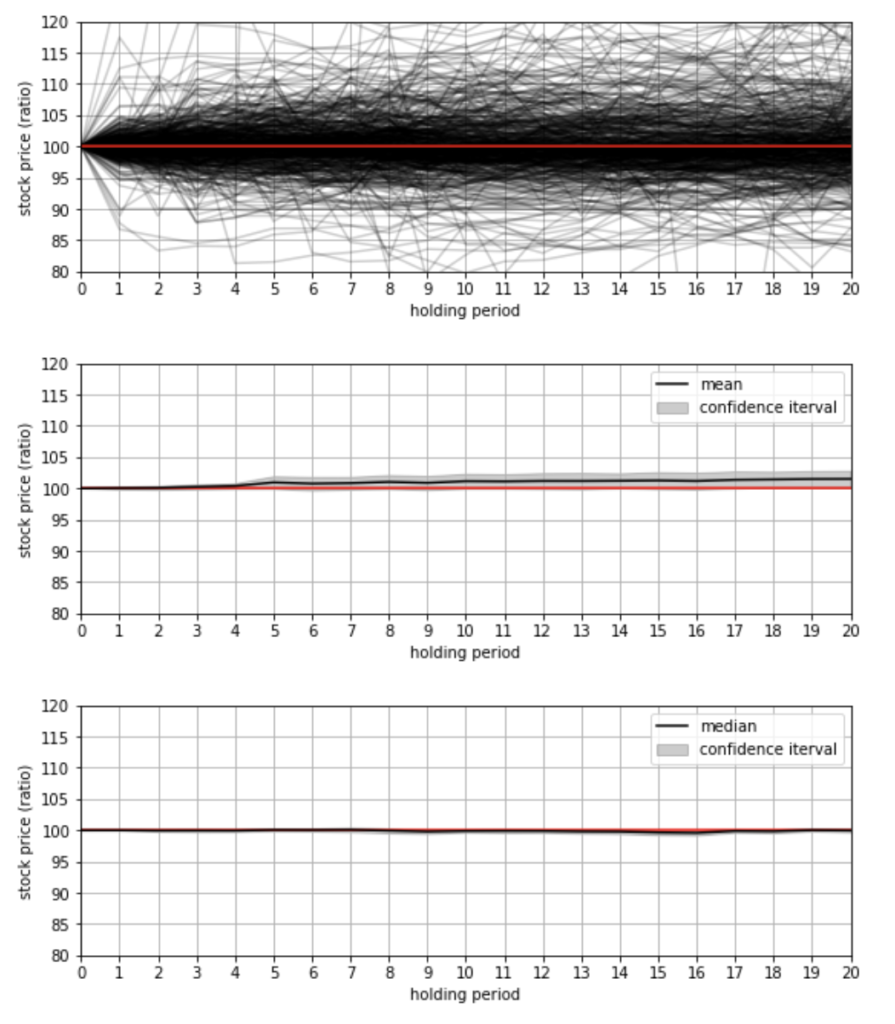
こちらは移動平均線の時と同じような結果となりました。
平均値で見れば上がっているのですが、中央値は全く変わりません。
これ、株価の上がり方下がり方は線形とみて良いのか？
RSI
RSIの買いシグナルからの株価推移。
# RSIの買いシグナルからの株価推移
# 各株価の推移
target_codes_prices = plot_holding_period_prices(
df=df_all,
start_date=start_date,
end_date=end_date,
codes=codes,
sampling_num=sampling_num,
holding_period=holding_period,
get_buy_signals_method=get_buy_signals_rsi
)
# 各保有時点での株価の平均値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='mean')
# 各保有時点での株価の中央値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='median')
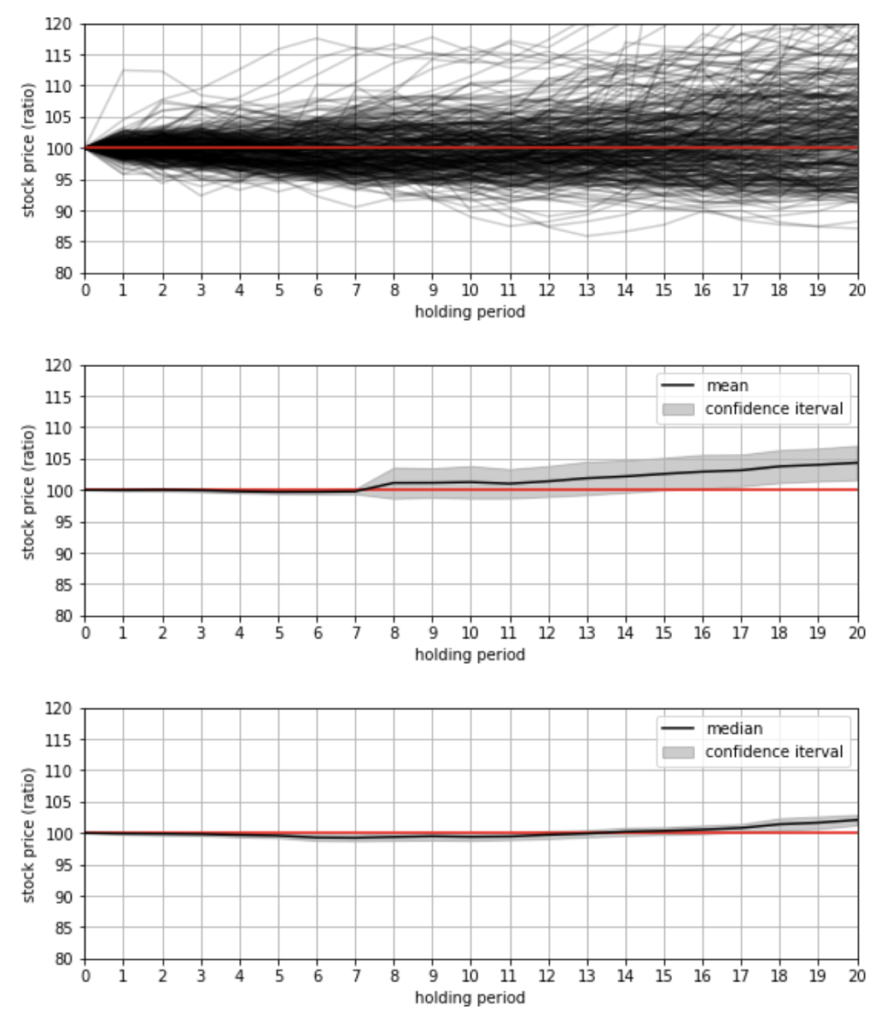
平均値どーした笑
中央値はあまり変わりは無さそうです。
ストキャスティクス
ストキャスティクスの買いシグナルからの株価推移。
# ストキャスティクスの買いシグナルからの株価推移
# 各株価の推移
target_codes_prices = plot_holding_period_prices(
df=df_all,
start_date=start_date,
end_date=end_date,
codes=codes,
sampling_num=sampling_num,
holding_period=holding_period,
get_buy_signals_method=get_buy_signals_stochastics
)
# 各保有時点での株価の平均値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='mean')
# 各保有時点での株価の中央値とブートストラップ信頼区間
plot_bootstrap_ci(target_codes_prices, holding_period=holding_period, stat='median')
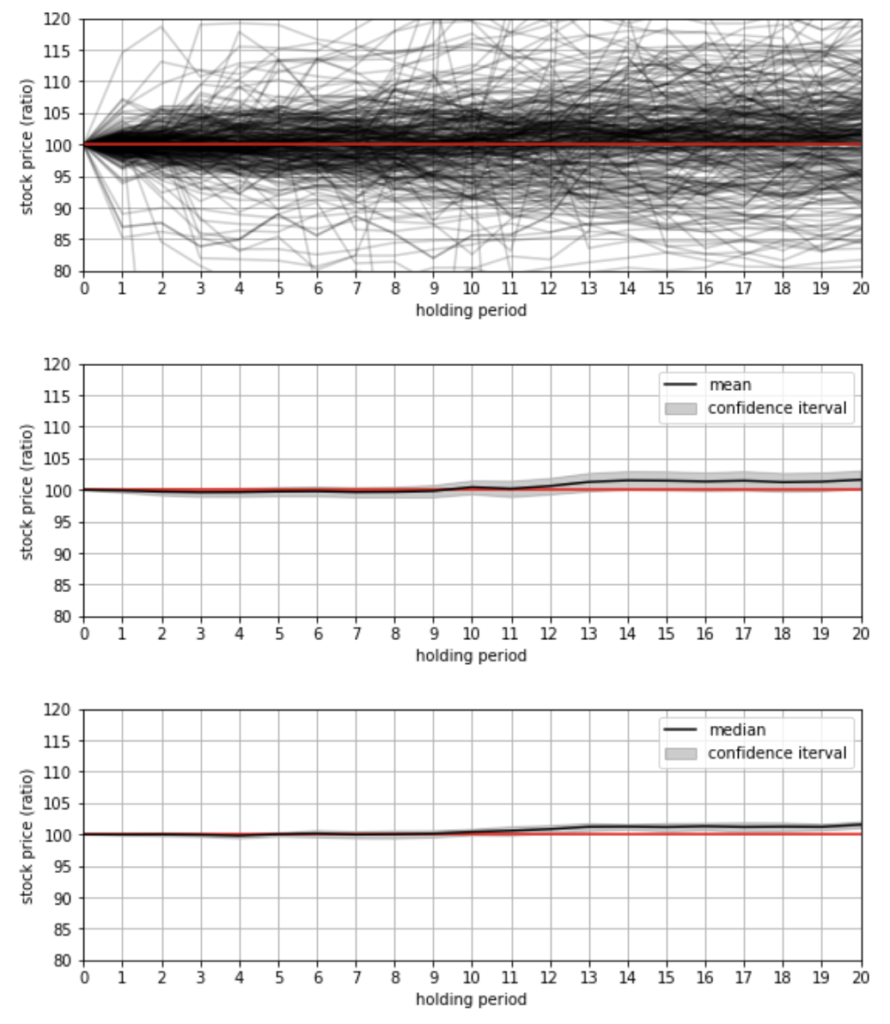
中央値の方も緩やかに上がってきている様子が見えます。
まとめ
以上、いくつかのテクニカル指標が表す買いシグナルからの株価推移について調べてみました。
こうして見ると、単体で使う分には、あまり目に見えて効果があるようには見えませんでした。
ちなみに、これを約3000件の銘柄すべてに対して、平均値を出してみると、外れ値に引き寄せられすぎて、ありえない方向にグラフが飛んでいってしまいます。
また、今回はブートストラップ法による信頼区間を試みましたが、そもそも復元抽出が、未来までの対象銘柄の株価の値動きの母集団からのサンプリングとみなせるのかも疑問です。
やはり市場の景気は刻一刻と変化していますので、それは同じ確率分布からサンプルを得られるとは限らないということだと思います。
ボリンジャーバンドは、確率の低い点に移動したとしてもいずれは確率の高いところに戻ってくるという使い方もするとは言っていましたが、どちらかといえば、それは均衡状態（確率分布）が仮定できない状態となったとみなすという使い方の方が、個人的にはしっくりきます。
今回のコードは以下にまとめました。
GitHub: https://github.com/Gin04gh/datascience/tree/master/stock_price_data_warehouse
しかし、そもそもテクニカル指標は、それぞれ単体で利用するというよりは、いくつかを組み合わせて使うことが効果的と言われています。
例えば、最近では下記のような書籍も出ています。
テクニカル指標のどのような組み合わせが良いのかについての書籍となります。
ちなみに上記も買いました←
やっぱり闇は深そうですが、一発を当てる必要はないので、せめて期待値が高い方法を見つけ、そこに投資し続けられるようになれば良いのになと思います。
コメント