状態空間モデルの勉強をしていましたので、実装について書きます。
PyStanやPyMC3の実装は、ある程度参考になる例が多いのですが、Edwardの実装例は見当たりませんでしたので、どんな感じになるか試しに実装してみました。
最近はめっきりPythonで分析を行うことが多く、Pythonでの状態空間モデルといえばStatsmodelsが有名かと思いますので、そちらの結果とも見比べてみます。
状態空間モデル
状態空間モデルは、時系列分析に用いられるモデルです。
といっても、状態空間モデル自体は幅広い概念であり、元々は制御工学で使われていた理論でした。
1970年代頃から、統計応用にも適用されるようになり、その後、金融データへの応用、例えば、ボラティリティの推定、債券価格やコモディティ価格のモデリングなどで、モデルの研究が進みました。
時系列分析のモデルといえば、AR/MA/ARMA/ARIMAなど様々ありますが、状態空間モデルは、ほとんどの時系列モデルを表現できる汎用性の高い時系列分析のモデルです。
時系列予測をさまざまな要因分解の結果として行なえるため、最近では、マーケティング分野において、売上に対する広告影響の構造把握などの適用事例もあります。
今回は実装について記しますので、詳細は書籍などを参照すると良い思います。
最近では、下記などがオススメです。
事例については、岩波DSの下記が参考になります。
今回は、状態空間モデルの中でも基礎となる、ローカルレベルモデルをPyStan、PyMC3、Edwardで実装してみました。
コードは以下にも置いておきました。
※Stanのログ出力も入ってしまって、とても長いので注意
GitHub: https://github.com/Gin04gh/datascience/blob/master/compare_state_space_model/notebook.ipynb
Statsmodelsで状態空間モデル
適当に時系列データを作成します。
import numpy as np
import matplotlib
import matplotlib.pylab as plt
%matplotlib inline
from tqdm import tqdm
y = np.cumsum(np.random.normal(size=100))
plt.plot(y)
plt.show()
他のライブラリであれば、モデルを実装 → パラメータを推定 → 結果を確認と段階を踏んで実装するのが普通です。
Statsmodelsでは、上記の一連の流れを UnobservedComponents 関数で、全て一気にやってくれます。
ローカルレベルでの推定は、引数に'local level'を指定します。
import statsmodels.api as sm
model = sm.tsa.UnobservedComponents(y, 'local level')
result = model.fit()
result.plot_components()
plt.show()
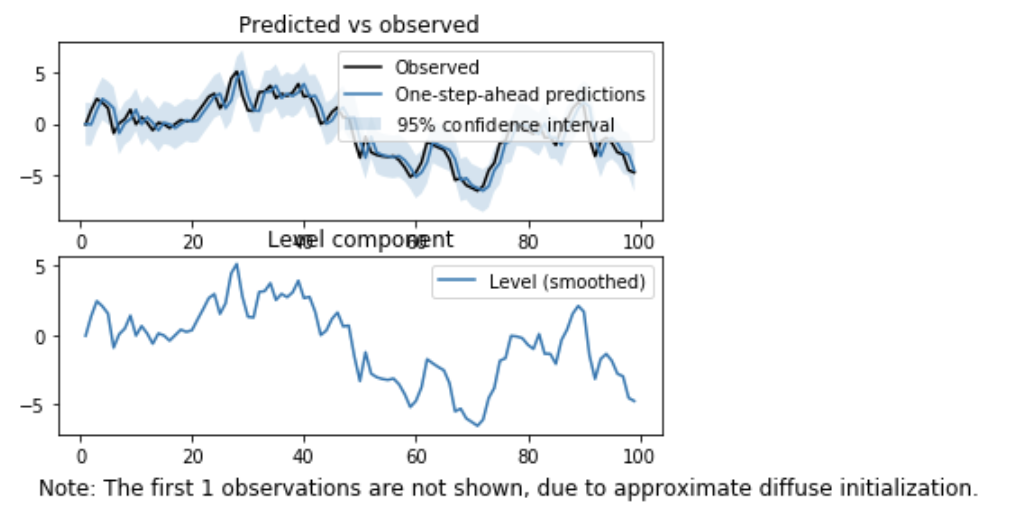
公式では、下記などのページ、
参考になるページとしては、下記などがあります。
PyStanで状態空間モデル
続いて、PyStanの場合です。
PyStanは、Stanコードでモデルを実装する必要があります。
別の言語の記法を覚えなければいけないのは面倒かもしれませんが、Stanは、Rから実行できるラッパーのRStanもあり、どちらもモデル部分は同じStanで書きますので、ネット上で参考になる例が多く見つかります。
ローカルレベルモデルを、モデル式で書くと、以下のようになります。
![]()
![]()
これをStanで記述した文字列を受け取って、Pythonから実行します。
import pystan
model = """
data {
int n; # サンプルサイズ
vector[n] y; # 時系列の値
}
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
real sigmaV; # 観測誤差の大きさ
real sigmaW; # 過程誤差の大きさ
}
model {
# 状態方程式
mu[1] ~ normal(muZero, sqrt(sigmaW));
for(i in 2:n) {
mu[i] ~ normal(mu[i-1], sqrt(sigmaW));
}
# 観測方程式
for(i in 1:n) {
y[i] ~ normal(mu[i], sqrt(sigmaV));
}
}
"""
fit = pystan.stan(model_code=model, data={'n': 100, 'y': y}, iter=1000, chains=1)
fit
Inference for Stan model: anon_model_4eca5dff070c8e9e2e8fbdc5e7560772.
1 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero -0.02 0.05 1.07 -2.16 -0.74 -0.03 0.72 1.99 500 1.0
mu[0] -0.04 0.01 0.23 -0.48 -0.15 -0.03 0.07 0.46 500 1.0
mu[1] -0.01 9.9e-3 0.22 -0.42 -0.15 -0.04 0.1 0.54 500 1.0
mu[2] 1.32 8.5e-3 0.19 0.89 1.21 1.34 1.44 1.71 500 1.0
mu[3] 2.36 0.01 0.23 1.85 2.25 2.38 2.48 2.82 500 1.0
mu[4] 2.04 9.3e-3 0.21 1.61 1.93 2.04 2.16 2.45 500 1.0
mu[5] 1.44 0.01 0.24 0.9 1.32 1.46 1.57 1.9 500 1.01
mu[6] -0.78 0.05 0.23 -1.13 -0.93 -0.82 -0.66 -0.24 22 1.03
mu[7] 0.03 9.7e-3 0.22 -0.41 -0.09 0.03 0.14 0.5 500 1.0
mu[8] 0.46 0.01 0.23 -0.01 0.34 0.46 0.59 0.93 500 1.0
mu[9] 1.28 9.8e-3 0.22 0.75 1.18 1.31 1.41 1.68 500 1.0
// 以下略
本来は、chainsを3以上に指定して、Rhatで収束しているか確認するべきかと思いますが...。
上記のようにfitを出力した時の結果は文字列ですが、Pythonで推定したパラメータを配列で取得したい場合は、extract関数を使います。
la = fit.extract()
pred = la['mu'].mean(axis=0)
mu_lower, mu_upper = np.percentile(la['mu'], q=[2.5, 97.5], axis=0)
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()
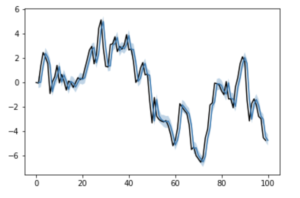
はい。
PyMC3で状態空間モデル
PyMC3の場合も、モデルを自分で実装します。
組み方としてはいろいろあると思いますが、例えば、以下のような形で書けると思います。
N = len(y)
T = 1000
with pm.Model() as model:
muZero = pm.Normal(name='muZero', mu=0.0, tau=1.0)
sigmaW = pm.InverseGamma(name='sigmaW', alpha=1.0, beta=1.0)
mu = [0]*N
mu[0] = pm.Normal(name='mu0', mu=muZero, tau=1/sigmaW)
for n in range(1, N):
mu[n] = pm.Normal(name='mu'+str(n), mu=mu[n-1], tau=1/sigmaW)
sigmaV = pm.InverseGamma(name='sigmaV', alpha=1.0, beta=1.0)
y_pre = pm.Normal('y_pre', mu=mu, tau=1/sigmaV, observed=y)
start = pm.find_MAP()
step = pm.NUTS()
trace = pm.sample(T, step, start=start)
分散パラメータの事前分布に逆ガンマ分布を使うのはあまり良くないらしいので、別途調整してください。
mu_samples = np.array([trace['mu'+str(i)] for i in range(N)])
pred = mu_samples.mean(axis=1)
mu_lower, mu_upper = np.percentile(mu_samples, q=[2.5, 97.5], axis=1)
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()
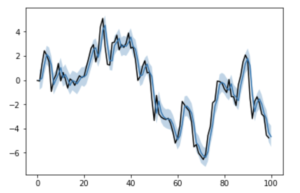
Stanに比べると情報が少ないために入りづらい印象があるPyMCですが、いざ書いてみるとPythonっぽくで意外とスッキリしている感はあります。
Edwardで状態空間モデル
Edwardでも、モデルを自前で実装する必要があります。
書き方は、Dustin氏のこの辺りのやりとりが参考になりました。
import tensorflow as tf
import edward as ed
from edward.models import Normal, InverseGamma, Empirical
N = len(y)
T = 1000
muZero = Normal(loc=0.0, scale=1.0)
sigmaW = InverseGamma(concentration=1.0, rate=1.0)
mu = [0]*N
mu[0] = Normal(loc=muZero, scale=sigmaW)
for n in range(1, N):
mu[n] = Normal(loc=mu[n-1], scale=sigmaW)
sigmaV = InverseGamma(concentration=1.0, rate=1.0)
y_pre = Normal(loc=tf.stack(mu), scale=sigmaV)
qmuZero = Empirical(tf.Variable(tf.zeros(T)))
qsigmaW = Empirical(tf.Variable(tf.zeros(T)))
qmu = [Empirical(tf.Variable(tf.zeros(T))) for n in range(N)]
qsigmaV = Empirical(tf.Variable(tf.zeros(T)))
latent_vars = {m: qm for m, qm in zip(mu, qmu)}
latent_vars[muZero] = qmuZero
latent_vars[sigmaW] = qsigmaW
latent_vars[sigmaV] = qsigmaV
inference = ed.HMC(latent_vars, data={y_pre: y})
inference.run(n_iter=T)
近似事後分布を設定する辺りなどがEdward特有の書き方ですが、それ以外はPyMCと似ている感じがしますね。
パラメータの取得も、以下のようにして取得しました。(これでいいのか?)
pred = np.zeros((len(y)), dtype=np.float32)
mu_lower = np.zeros((len(y)), dtype=np.float32)
mu_upper = np.zeros((len(y)), dtype=np.float32)
for i, _qmu in enumerate(tqdm(qmu)):
qmu_sample = _qmu.sample(1000).eval()
_pred = qmu_sample.mean()
_mu_lower, _mu_upper = np.percentile(qmu_sample, q=[2.5, 97.5], axis=0)
pred[i] = _pred
mu_lower[i] = _mu_lower
mu_upper[i] = _mu_upper
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()
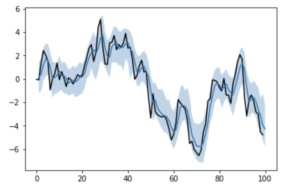
良い感じに推定してくれました。
PyStanと同じようにMCMCしたつもりですが、区間がやたら広くなってしまっているのは、なんでかなーとは思いますが...。
事前分布を自分で設定している辺りなどが、影響があるのでしょうか。
また、収束判定などを入れていないはずなので、そこは別途追加する必要があると思います。
感想
やっぱ、Stanで良さそう←
やはりモデルの実装例の情報がStanの方がたくさん見つかるので、いろいろなパターンを素早く吸収することができます。
Edwardが他のライブラリよりも圧倒的に早いと言われている理由はGPUですので、Stanではかなりの時間がかかりそうなモデルの推定に関して、GPUを使って実行してみた時の比較などを検証してみたいところです。





コメント