クレジットカード不正利用予測モデルを作成・評価してみた

表題の通り、Kaggleデータセットに、クレジットカードの利用履歴データを主成分化したカラムが複数と、それが不正利用であったかどうかラベル付けされているデータがあります。

- https://www.kaggle.com/mlg-ulb/creditcardfraud

今回は普通に、このデータを用いてクレジットカードの不正利用予測モデルを構築して評価するまでを実装してみます。

ソースはすべて以下のGitHubにノートブックのまま上げました。

GitHub: https://github.com/Gin04gh/datascience/blob/master/kaggle_dataset_credit_card_fraud_detection/notebook.ipynb

Contents

データの確認
データサンプリング
特徴量選択
モデル学習
モデル評価
データの傾向についての分析
まとめ

データの確認

上記で述べたように、元々特徴量はほとんどが主成分化されているため、どのカラムがどういった内容を表すのかは不明です。

また、欠損値もありません。

クラスについて集計をしてみますと、

データ件数	不正利用フラグ=1の件数	不正利用データ確率
284,807件	492件	0.00173

と、かなり不均衡なデータになっています。

相関行列のヒートマップを可視化してみると、

df = pd.read_csv('./data/creditcard.csv')
plt.figure(figsize=(18,15))
sns.heatmap(df.corr(), annot=True, vmax=1, vmin=-1, fmt='.1f', cmap=cm)
plt.show()

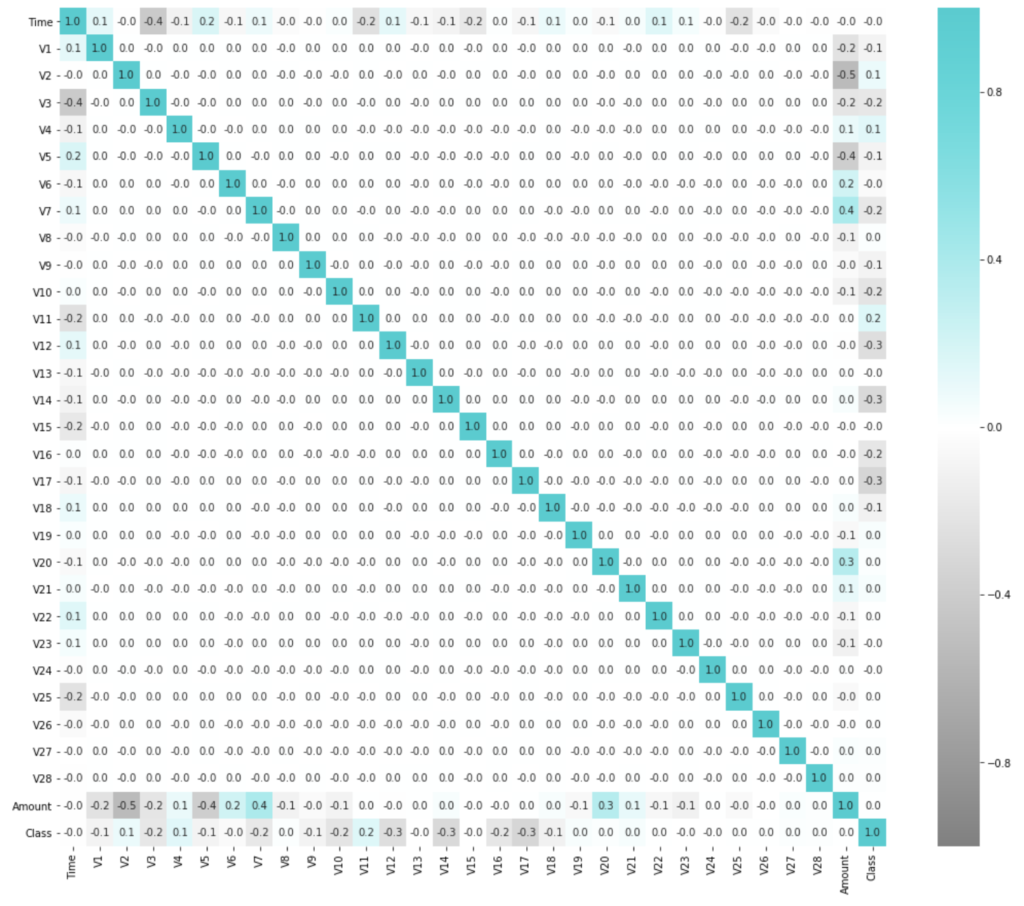
といった感じ。（不正利用クラスのカラムは最下段の Class の項目）

データサンプリング

上記の通り、データがかなり偏っていますので、ちゃんとモデルを学習させられるように、データをサンプリングして偏りを揃えます。

アンダーサンプリングやオーバーサンプリングなどが揃っている imblearn を使います。

from imblearn import under_sampling, over_sampling

cols = df.columns.tolist()
cols.remove('Class')

positive_cnt = int(df['Class'].sum())
rus = under_sampling.RandomUnderSampler(sampling_strategy={0:positive_cnt, 1:positive_cnt}, random_state=0)
data_x_sample, data_y_sample  = rus.fit_sample(df[cols], df[['Class']])

len(data_x_sample), len(data_y_sample), df['Class'].sum()
"""
(984, 984, 492)
"""

不正取引 Class = 1 が圧倒的に少ないので、これに合わせるように、不正取引でないデータをアンダーサンプリングしました。

特徴量選択

分類モデルの学習に効く特徴量を探すため、scikit-learnに実装されている RFECV を使います。

再帰的特徴除去（Recursive Feature Elimination; RFE）は、変数減少法と同じく、最初に全ての特徴量を使ってモデルを学習し、最も重要度の低いを特徴量を除去して、性能を再計算するという処理を繰り返していきます。

重要度の指標には feature_importances や coef が使われるようです。

これを交差検証の中で行うのが RFECV になります。

# 特徴量を選択する
feature_importance_models = [
    ensemble.AdaBoostClassifier(),
    ensemble.ExtraTreesClassifier(),
    ensemble.GradientBoostingClassifier(),
    ensemble.RandomForestClassifier(),
    tree.DecisionTreeClassifier(),
    XGBClassifier()
]

scoring = ['accuracy']
df_rfe_cols_cnt = pd.DataFrame(columns=['cnt'], index=cols)
df_rfe_cols_cnt['cnt'] = 0

for i, model in tqdm(enumerate(feature_importance_models), total=len(feature_importance_models)):
    rfe = feature_selection.RFECV(model, step=3)
    rfe.fit(data_x_sample, data_y_sample)
    rfe_cols = df[cols].columns.values[rfe.get_support()]
    df_rfe_cols_cnt.loc[rfe_cols, 'cnt'] += 1

df_rfe_cols_cnt.plot(kind='bar', color=base_color, figsize=(15, 5))
plt.show()

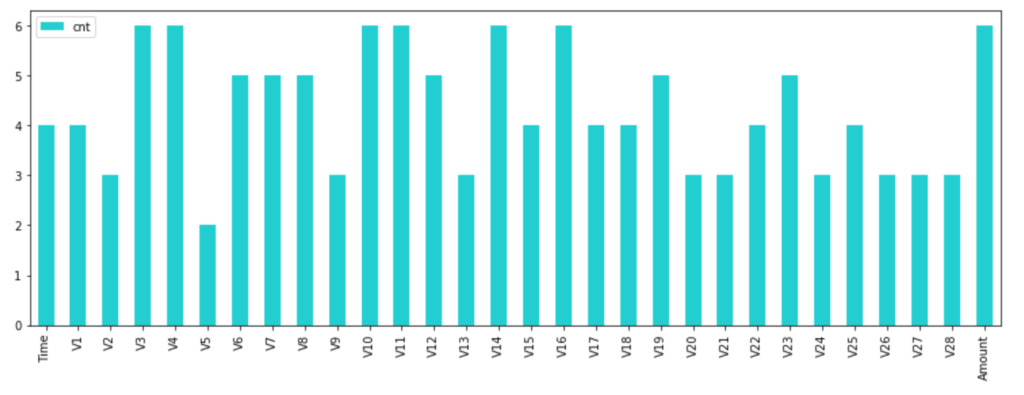
どの変数がどのくらい選ばれたかが分かります。

上記6つのモデル中4つ以上のモデルから選択された特徴量を使うことにしました。

x_cols = df_rfe_cols_cnt[df_rfe_cols_cnt['cnt'] >= 4].index
x_cols
"""
Index(['Time', 'V1', 'V3', 'V4', 'V6', 'V7', 'V8', 'V10', 'V11', 'V12', 'V14',
       'V15', 'V16', 'V17', 'V18', 'V19', 'V22', 'V23', 'V25', 'Amount'],
      dtype='object')
"""

モデル学習

ハイパーパラメータをグリッドサーチさせた複数のモデルに関する投票モデルを作ってみます。

最初に、複数のモデルについて学習させてみます。

後で精度を見ながらモデルを選びますので、ひとまず思いついたものをぶっ込んでみる。

# 特徴量を選択して、複数のモデルで精度を調査する
models = [
    #Ensemble Methods
    ensemble.AdaBoostClassifier(),
    ensemble.BaggingClassifier(),
    ensemble.ExtraTreesClassifier(),
    ensemble.GradientBoostingClassifier(),
    ensemble.RandomForestClassifier(),

    #Gaussian Processes
    gaussian_process.GaussianProcessClassifier(),

    #GLM
    linear_model.LogisticRegressionCV(),
    linear_model.RidgeClassifierCV(),

    #Navies Bayes
    naive_bayes.BernoulliNB(),
    naive_bayes.GaussianNB(),

    #Nearest Neighbor
    neighbors.KNeighborsClassifier(),

    #Trees
    tree.DecisionTreeClassifier(),
    tree.ExtraTreeClassifier(),

    #Discriminant Analysis
    discriminant_analysis.LinearDiscriminantAnalysis(),
    discriminant_analysis.QuadraticDiscriminantAnalysis(),

    #xgboost
    XGBClassifier()
]

df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']

for model in tqdm(models):
    name = model.__class__.__name__

    cv_rlts = model_selection.cross_validate(model, data_x_sample, data_y_sample, scoring=scoring, cv=10, return_train_score=True)

    for i in range(10):
        s = pd.Series([name, cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name=name+str(i))
        df_compare = df_compare.append(s)

plt.figure(figsize=(12,8))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()

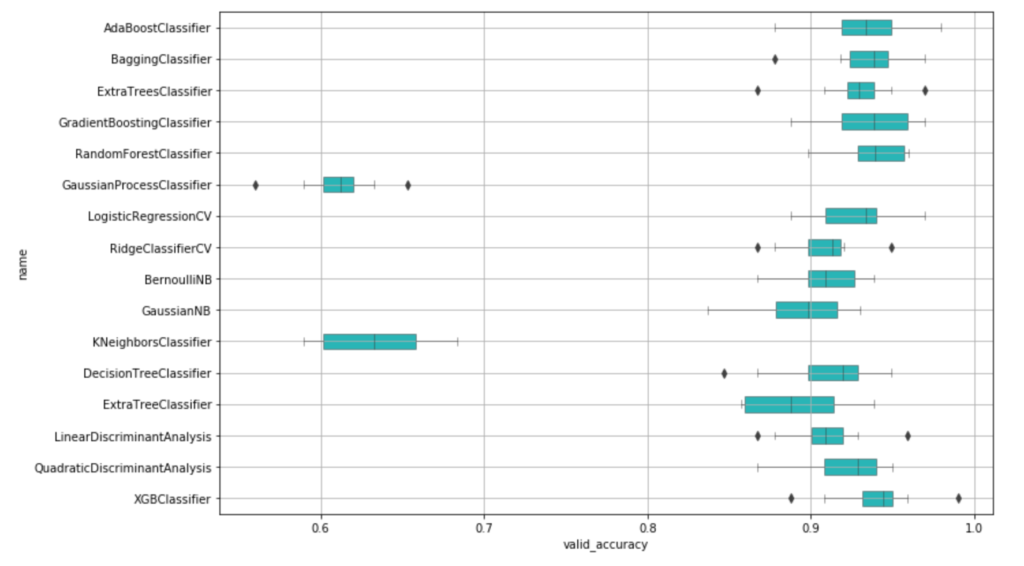
安定のXGBoostに続いて、AdaBoost、バギング、勾配Boosting辺りが良いようです。

valid_accuracy で平均してソートすると、

df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)

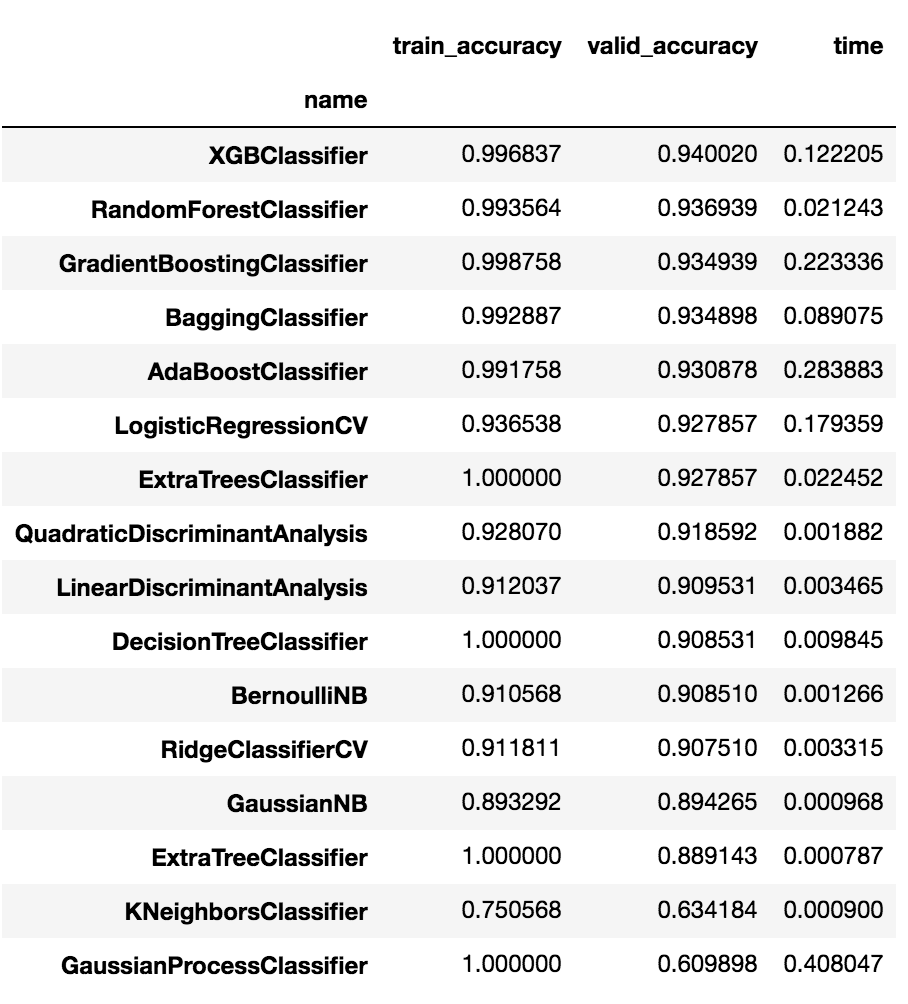
な感じです。

さらにこの中から精度の良いモデルを複数選んで、ひとまずハイパーパラメータをデフォルトのままで投票モデルを学習させてみます。

# 精度の良いモデルを選んで、投票モデルを学習
vote_models = [
    #Ensemble Methods
    ('abc', ensemble.AdaBoostClassifier()),
    ('bc', ensemble.BaggingClassifier()),
    ('etsc', ensemble.ExtraTreesClassifier()),
    ('gbc', ensemble.GradientBoostingClassifier()),
    ('rfc', ensemble.RandomForestClassifier()),

    #Gaussian Processes
    #('gpc', gaussian_process.GaussianProcessClassifier()),

    #GLM
    ('lrcv', linear_model.LogisticRegressionCV()),
    #('rccv', linear_model.RidgeClassifierCV()), # unable soft voting

    #Navies Bayes
    #('bnb', naive_bayes.BernoulliNB()),
    #('gnb', naive_bayes.GaussianNB()),

    #Nearest Neighbor
    #('knc', neighbors.KNeighborsClassifier()),

    #Trees
    #('dtc', tree.DecisionTreeClassifier()),
    #('etc', tree.ExtraTreeClassifier()),

    #Discriminant Analysis
    #('lda', discriminant_analysis.LinearDiscriminantAnalysis()),
    #('qda', discriminant_analysis.QuadraticDiscriminantAnalysis()),

    #xgboost
    ('xgbc', XGBClassifier())
]

df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']

vote_hard_model = ensemble.VotingClassifier(estimators=vote_models, voting='hard')
cv_rlts = model_selection.cross_validate(vote_hard_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
    s = pd.Series(['hard', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='hard'+str(i))
    df_compare = df_compare.append(s)

vote_soft_model = ensemble.VotingClassifier(estimators=vote_models , voting='soft')
cv_rlts = model_selection.cross_validate(vote_soft_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
    s = pd.Series(['soft', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='soft'+str(i))
    df_compare = df_compare.append(s)

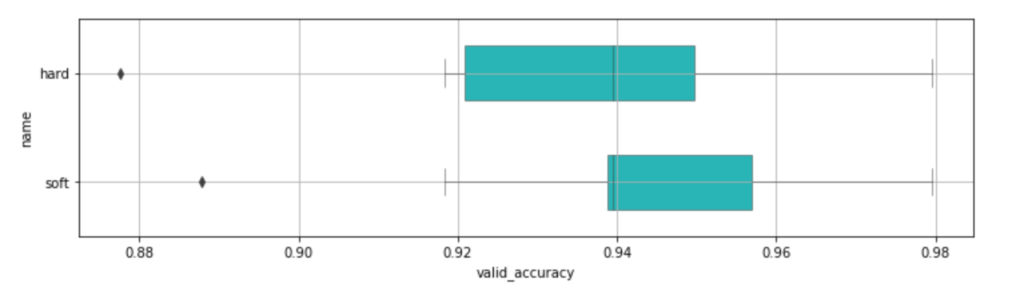
plt.figure(figsize=(12,3))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()

df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)

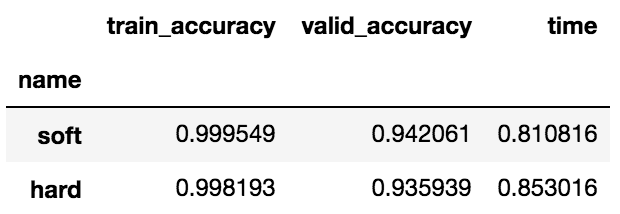
後にスコアリングしたいので predict_proba が使える soft しか使いませんが、一応 hard も出しています。

hard は単純に利用した複数のモデルによる多数決でクラスを予測、 soft は利用したモデルのそれぞれの predict_proba による予測確率の平均値からクラスを予測しています。

さて、さらにグリッドサーチを行って、各モデルで最適なハイパーパラメータを選択してみます。

# 各モデルのハイパーパラメータをグリッドサーチ

grid_n_estimator = [10, 50, 100, 300]
grid_ratio = [.1, .25, .5, .75, 1.0]
grid_learn = [.01, .03, .05, .1, .25]
grid_max_depth = [2, 4, 6, 8, 10, None]
grid_min_samples = [5, 10, .03, .05, .10]
grid_criterion = ['gini', 'entropy']
grid_bool = [True, False]
grid_seed = [0]

grid_param = [
    #AdaBoostClassifier
    [{
        'n_estimators': grid_n_estimator, #default=50
        'learning_rate': grid_learn, #default=1
        #'algorithm': ['SAMME', 'SAMME.R'], #default=’SAMME.R
        'random_state': grid_seed
    }],

    #BaggingClassifier
    [{
        'n_estimators': grid_n_estimator, #default=10
        'max_samples': grid_ratio, #default=1.0
        'random_state': grid_seed
     }],

    #ExtraTreesClassifier
    [{
        'n_estimators': grid_n_estimator, #default=10
        'criterion': grid_criterion, #default=”gini”
        'max_depth': grid_max_depth, #default=None
        'random_state': grid_seed
     }],

    #GradientBoostingClassifier
    [{
        #'loss': ['deviance', 'exponential'], #default=’deviance’
        'learning_rate': [.05], #default=0.1
        'n_estimators': [300], #default=100
        #'criterion': ['friedman_mse', 'mse', 'mae'], #default=”friedman_mse”
        'max_depth': grid_max_depth, #default=3
        'random_state': grid_seed
     }],

    #RandomForestClassifier
    [{
        'n_estimators': grid_n_estimator, #default=10
        'criterion': grid_criterion, #default=”gini”
        'max_depth': grid_max_depth, #default=None
        'oob_score': [True], #default=False
        'random_state': grid_seed
     }],

    #LogisticRegressionCV
    [{
        'fit_intercept': grid_bool, #default: True
        #'penalty': ['l1','l2'],
        'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'], #default: lbfgs
        'random_state': grid_seed
     }],

    # ExtraTreeClassifier
    [{}],

    # LinearDiscriminantAnalysis
    [{}],

    #XGBClassifier
    [{
        'learning_rate': grid_learn, #default: .3
        'max_depth': [1,2,4,6,8,10], #default 2
        'n_estimators': grid_n_estimator,
        'seed': grid_seed
     }]
]

for model, param in tqdm(zip(vote_models, grid_param), total=len(vote_models)):
    best_search = model_selection.GridSearchCV(estimator=model[1], param_grid=param, scoring='roc_auc')
    best_search.fit(data_x_sample, data_y_sample)

    best_param = best_search.best_params_
    model[1].set_params(**best_param)

上記、実行後、再び投票モデルを学習させます。

# グリッドサーチしたハイパーパラメータを使ったモデルで、投票モデルを学習
df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']

vote_hard_model = ensemble.VotingClassifier(estimators=vote_models, voting='hard')
cv_rlts = model_selection.cross_validate(vote_hard_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
    s = pd.Series(['hard', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='hard'+str(i))
    df_compare = df_compare.append(s)

vote_soft_model = ensemble.VotingClassifier(estimators=vote_models , voting='soft')
cv_rlts = model_selection.cross_validate(vote_soft_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
    s = pd.Series(['soft', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='soft'+str(i))
    df_compare = df_compare.append(s)

plt.figure(figsize=(12,3))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()

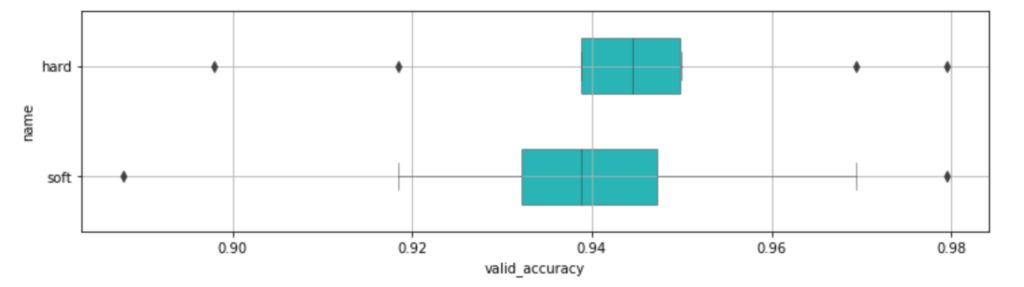
df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)

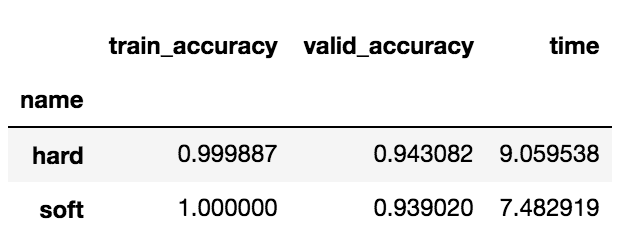
これはあまり効果はなさそうですね。

hard については上がっているものの、 soft に関しては下がってしまいました。

この辺りは割と、最後にわずかの数パーセントが上がってくれればといったくらいの気持ちだったりします。

モデル評価

改めて精度を確認してみます。

train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)

vote_soft_model.fit(train_x, train_y)
pred = vote_soft_model.predict(valid_x)

fig, axs = plt.subplots(ncols=2,figsize=(15,5))
sns.heatmap(metrics.confusion_matrix(valid_y, pred), vmin=0, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Accuracy: {}'.format(metrics.accuracy_score(valid_y, pred)))
fpr, tpr, thresholds = metrics.roc_curve(valid_y, pred)
axs[1].plot(fpr, tpr, color=base_color)
axs[1].set_title('ROC curve')
axs[1].set_xlabel('False Positive Rate')
axs[1].set_ylabel('True Positive Rate')
axs[1].grid(True)
plt.show()

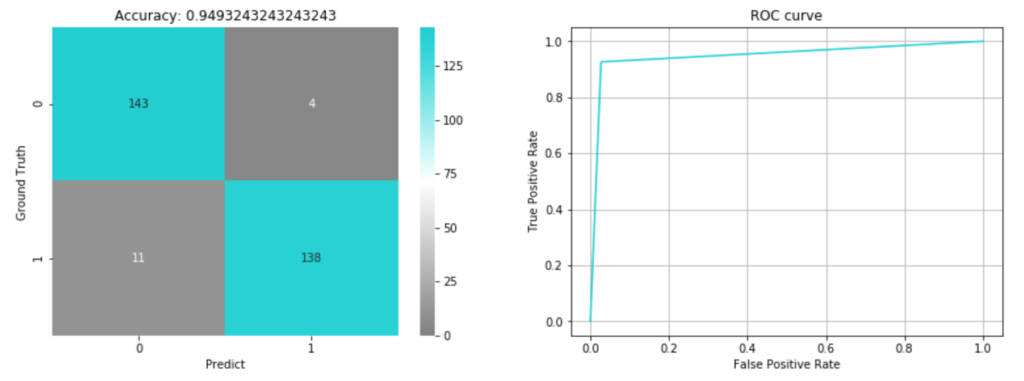
混合行列とROC曲線を可視化しました。

検証データに対する精度は 0.949 となりました。

ただし、上記の検証データは、実際には、Ground Truthが 0 のデータの方がたくさん存在する不均衡データですので、サンプリングで調整した分を戻して混合行列を出してみます。

# 上記の結果を、実際の不均衡の比率に合わせた結果の混合行列
confusion_matrix = metrics.confusion_matrix(valid_y, pred)
confusion_matrix_scaled = np.array([
    confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
    confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
], dtype=np.int32)

plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_scaled, vmin=0, annot=True, fmt='d', cmap=cm)
plt.xlabel('Predict')
plt.ylabel('Ground Truth')
plt.show()

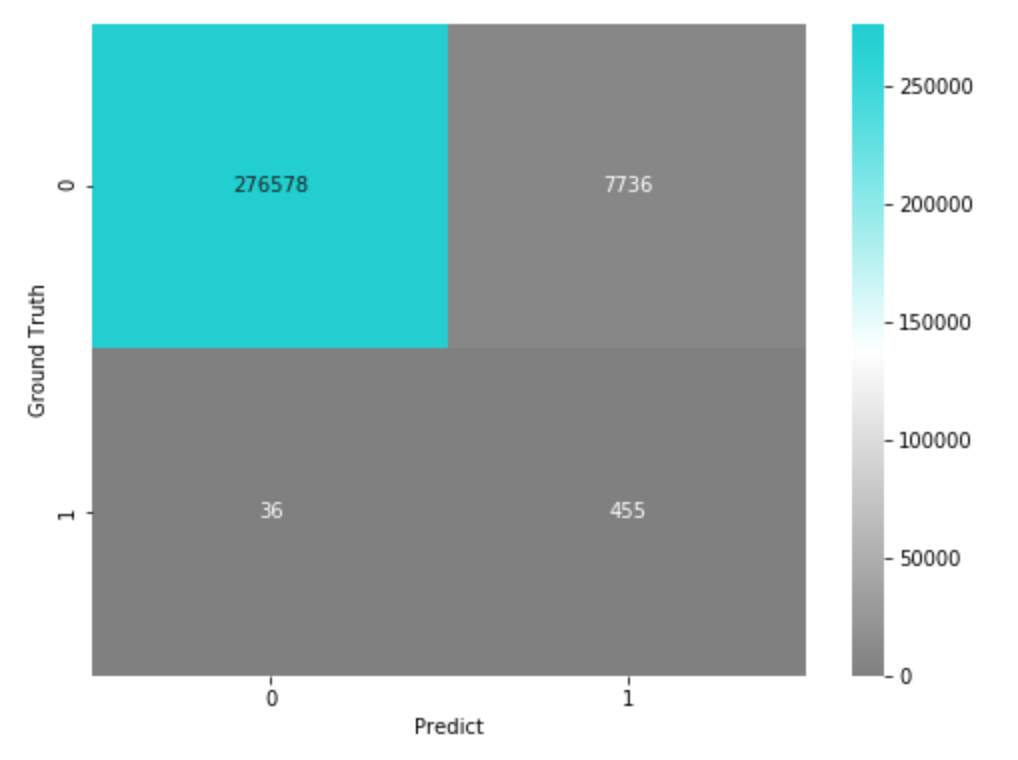
実際の運用時には、このくらいのFalse Positive, False Negativeが発生するという感じですね。

今回はさらに、いろいろと設定を仮定した上で、それぞれの場合の損益の効果まで考えてみます。

クレジットカードといえば、盗難保険がついていますよね。

不正利用により顧客が失った金額は、こういった盗難保険などといった形で、クレジットカード会社が負担するようになっているそうです。

- https://news.cardmics.com/entry/tonan-hoken-detail/

ということは、不正利用がないと予測したけども、実際に不正利用があった時には、不正利用を見逃したことになり、結果負担コストが発生すると考えられます。 $=cost_{fn}(account)$

なので、保険会社的には、不正利用を予測することで、被害を抑えたいというモチベーションがあるわけですね。

では仮に、不正利用があると予測し、実際に不正利用されていた場合には、失うはずであった金額を抑えることが出来たと考えてみます。 $=benefit_{tp}(account)$

逆に、不正利用があると予測したけども、実際に不正利用はなかった時には、そのアカウントに迷惑をかけることになり、利用停止を解除するコストも発生すると考えてみます。 $=cost_{fp}(account)$

- https://kurumicat.com/zakki015

また、不正利用がないと予測して、実際に不正利用はない時の1アカウント当たりの平均利益も考えてみます。 $=benefit_{tn}(account)$

このようにして考えた場合に、損益行列は

$benefit_{tn}(True Negative)$	$cost_fp(False Positive)$
$cost_{fn}(False Negative)$	$benefit_{tp}(True Positive)$

と表せます。

ではさらに仮にですが、

利用停止を解除するコストとして1アカウント当たり平均コスト額が1万円
不正利用を検知できず悪用されてしまった場合の1アカウント当たりの平均負担額が100万円

かかるとしてみます。

そうすると、

$benefit_{tn}(account) = 0$
$cost_{fp}(account) = −1{\times}account$
$cost_{fn}(account) = −100{\times}account$
$benefit_{tp}(account) = 0$

と置けそうです。

$benefit_{tp}$ は不正利用を未然に防ぐことができた金額が100万円と考えられますが、プラスで計算してしまうと $cost_{fn}$ と二重で計算してしまうことになるので、片方だけ計算するとして、こちらは0としておきます。

実際にはこういったそれぞれの場合の利益や損失の規模感をクライアントや担当者にアリングできるかが重要になると思いますが、ひとまず上記の仮定のまま進めてみると、実際の不均衡データに対して、モデルが予測した時の最終的な損益行列は

def benefit_tn(account):
    return 0*account

def cost_fp(account):
    return -1*account

# 不正利用を検知できずに悪用されてしまったと考える場合
def cost_fn(account):
    return -100*account

def benefit_tp(account):
    return 0*account

# 不正利用を未然に防ぐことができたと考える場合
def cost_fn2(account):
    return 0*account

def benefit_tp2(account):
    return 100*account

tn, fp, fn, tp = confusion_matrix_scaled.flatten()

fig, axs = plt.subplots(ncols=2, figsize=(14, 5))

bc_matrix = np.array([
    [benefit_tn(tn), cost_fp(fp)],
    [cost_fn(fn), benefit_tp(tp)],
], dtype=np.int)

sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))

bc_matrix = np.array([
    [benefit_tn(tn), cost_fp(fp)],
    [cost_fn2(fn), benefit_tp2(tp)],
], dtype=np.int)

sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[1])
axs[1].set_xlabel('Predict')
axs[1].set_ylabel('Ground Truth')
axs[1].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))

plt.show()

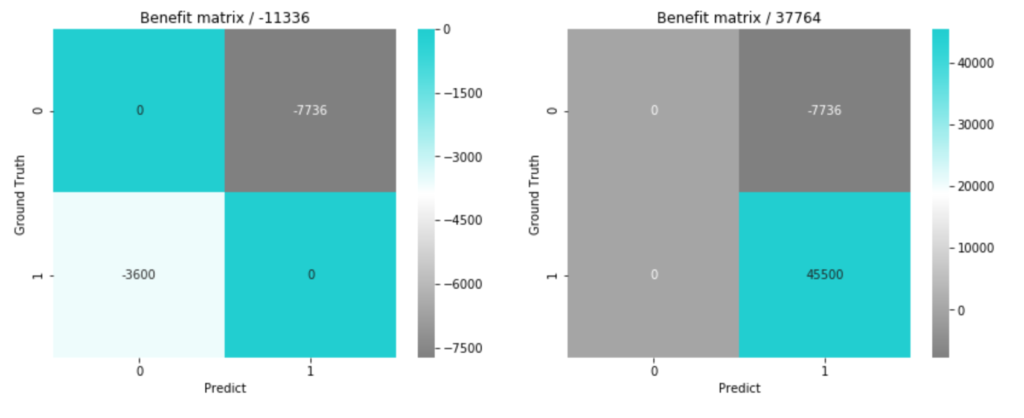
となりそうなことが分かりました。

predict では予測確率が0.5以上でクラス判定としているので、この予測確率をどのくらいの閾値に設定しておけば、利益が最大となるかを可視化してみます。

# 利益曲線を作る
pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1] # 不正利用である確率

def get_expected_benefit(confusion_matrix):
    confusion_matrix_scaled = np.array([
        confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
        confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
    ], dtype=np.int32)
    tn, fp, fn, tp = confusion_matrix_scaled.flatten()
    return benefit_tn(tn)+cost_fp(fp)+cost_fn(fn)+benefit_tp(tp)

thresholds = np.linspace(0, 1, 101)
benefits = np.zeros(len(thresholds))

for i, thresh in enumerate(thresholds):
    pred_tmp = np.zeros((len(valid_y)))
    pred_tmp[np.where(pred_prob > thresh)] = 1
    confusion_matrix = metrics.confusion_matrix(valid_y, pred_tmp)
    benefits[i] = get_expected_benefit(confusion_matrix)

plt.plot(thresholds, benefits, color=base_color)
plt.xlabel('Threshold')
plt.ylabel('Benefit')
plt.title('Benefit curve')
plt.grid()
plt.show()

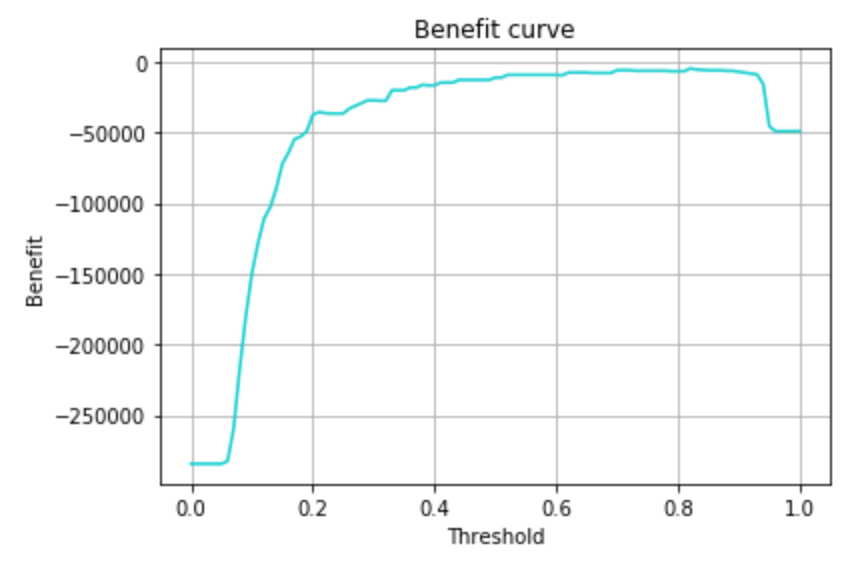
学習データと検証データのセットを何パターンか試してみるため、何回かの検証データを使って信頼区間を出してみて、その上で、最大利益となる閾値を求めました。

trial_num = 20

thresholds = np.linspace(0, 1, 101)
benefits = np.zeros((trial_num, len(thresholds)))

for trial in tqdm(range(trial_num)):
    train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3)
    vote_soft_model.fit(train_x, train_y)
    pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1]

    for i, thresh in enumerate(thresholds):
        pred_tmp = np.zeros((len(valid_y)))
        pred_tmp[np.where(pred_prob > thresh)] = 1
        confusion_matrix = metrics.confusion_matrix(valid_y, pred_tmp)
        benefits[trial, i] = get_expected_benefit(confusion_matrix)

plt.figure(figsize=(10,6))

lower_benefit, median_benefit, upper_benefit = mstats.mquantiles(benefits, [0.1, 0.5, 0.9], axis=0)

plt.plot(thresholds, median_benefit, color=base_color)
plt.fill_between(thresholds, upper_benefit, lower_benefit, color=base_color, alpha=0.3, linewidth=0)

max_benefit_point = thresholds[median_benefit == median_benefit.max()][0]
plt.vlines([max_benefit_point], benefits.min(), benefits.max(), color='black', linestyles='--')

plt.xlabel('Threshold')
plt.ylabel('Benefit')
plt.title('Benefit curve / interval 0.1--0.9')
plt.grid()
plt.show()

max_benefit_point

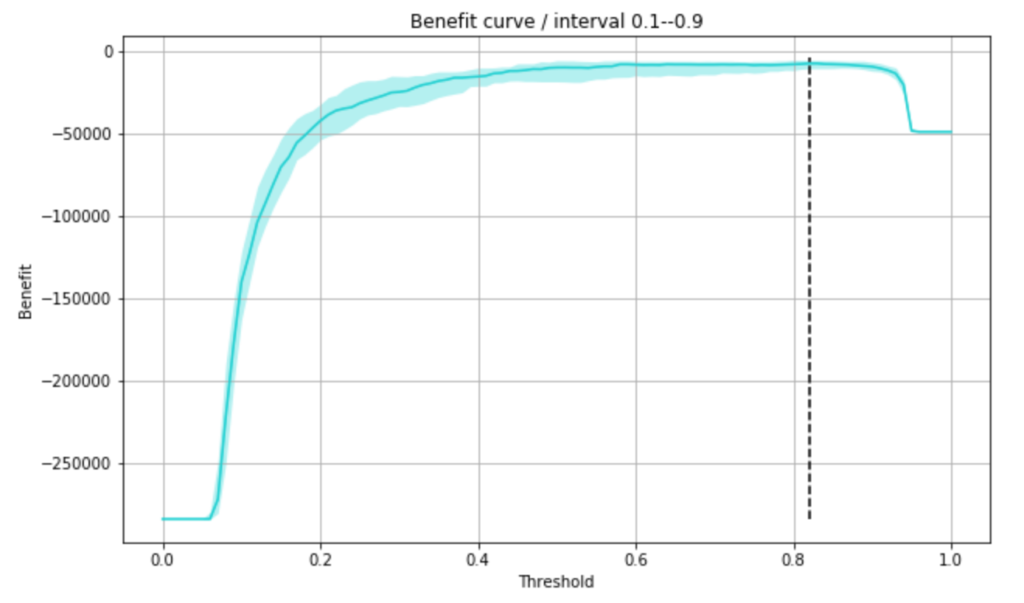
0.8200000000000001

不正利用である確率が、上記閾値を超えているものに不正利用予測をすれば、利益が最大になるとのことなので、この閾値で再度損益行列を出してみます。

# 利益を最大にする閾値の時の損益行列

prob_thresh = 0.82

train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)

vote_soft_model.fit(train_x, train_y)

pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1]
pred = np.zeros((len(valid_y)))
pred[np.where(pred_prob > prob_thresh)] = 1

confusion_matrix = metrics.confusion_matrix(valid_y, pred)
confusion_matrix_scaled = np.array([
    confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
    confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
], dtype=np.int32)

tn, fp, fn, tp = confusion_matrix_scaled.flatten()

fig, axs = plt.subplots(ncols=2, figsize=(14, 5))

bc_matrix = np.array([
    [benefit_tn(tn), cost_fp(fp)],
    [cost_fn(fn), benefit_tp(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))

bc_matrix = np.array([
    [benefit_tn(tn), cost_fp(fp)],
    [cost_fn2(fn), benefit_tp2(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[1])
axs[1].set_xlabel('Predict')
axs[1].set_ylabel('Ground Truth')
axs[1].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))

plt.show()

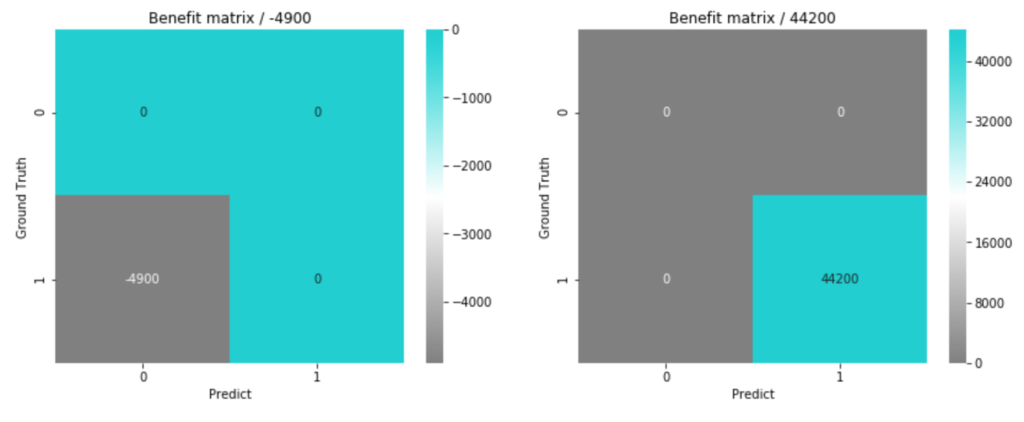
この仮定の場合においては、False Positiveを抑える（Precisionを高めにしておく）方が、コストがかからないということになりました。

あとは既存で使われている予測モデルに対しても同様の分析を行って比較ができれば、どのくらいの費用対効果があるのかが分かりやすく示せるのではないかと思います。

データの傾向についての分析

ついでに、主成分の中身はわからないんですが、以下、決定木モデルによる主成分の傾向を分析してみました。

# 決定木による傾向分析
train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)

decision_tree = tree.DecisionTreeClassifier()
decision_tree.fit(train_x, train_y)

dot_data = StringIO()
tree.export_graphviz(decision_tree, out_file=dot_data, feature_names=x_cols, max_depth=5)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf('graph.pdf')
Image(graph.create_png())

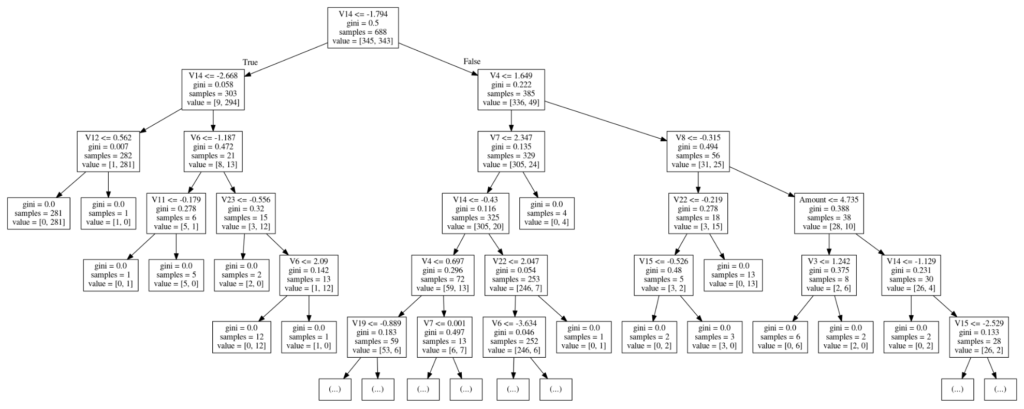
何か、1つ目の切り分けルールでかなり分けられていることが、ジニ係数などを確認してみても分かります。

そこで、データから1つ目ルールで切り分けられた集団ごとの不正予測の比率を確認してみます。

df_tmp = df.copy()

df_tmp.loc[df_tmp['V14'] <= -1.794, 'V14 <= -1.794'] = 1
df_tmp.loc[~(df_tmp['V14'] <= -1.794), 'V14 <= -1.794'] = 0
df_tmp['V14 <= -1.794'] = df_tmp['V14 <= -1.794'].astype(np.int)

g = sns.factorplot(x='V14 <= -1.794', y='Class',data=df_tmp, kind='bar', palette=[base_color2, base_color])
g = g.set_ylabels('Fraud Probability')
plt.hlines([df_tmp['Class'].sum()/len(df_tmp)], -1, 2, color='black', linestyles='--')
plt.show()

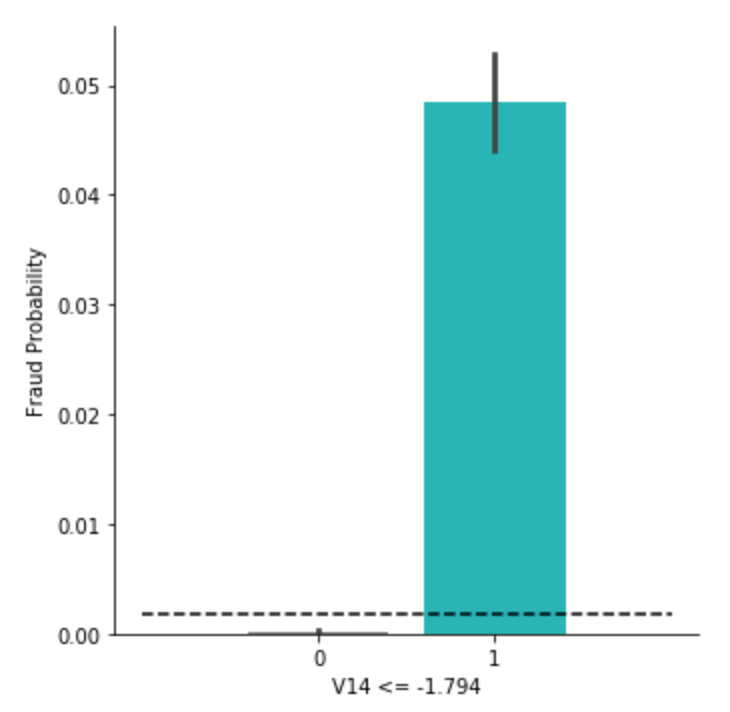
黒の点線が、もともとの不正利用の確率 0.00173 を指しています。

それよりもルールで切り分けられた集団ごとに確率を出してみると、かなり異なることが分かりました。

というか、片方はもはや潰れてるし。

ちゃんと値を出してみたものが以下。

df_tmp[df_tmp['V14 <= -1.794'] == 1]['Class'].sum()/len(df_tmp[df_tmp['V14 <= -1.794'] == 1]) # 0.04848553345388788
df_tmp[df_tmp['V14 <= -1.794'] == 0]['Class'].sum()/len(df_tmp[df_tmp['V14 <= -1.794'] == 0]) # 0.00022829478292065125

冒頭の相関行列でも他の成分に比べて絶対値が大きめですし、意外と生データにおいて、不正利用かどうかを判断しやすいような項目があり、それが自然とこの主成分にまとめられたのかもしれません。

まとめ

ただのデータセットでしたが、今回は、意思決定者に対して、どこまでのモデル評価を実施できれば良いだろうかといったところを念頭に取り組んでみました。

損益行列あたりの話は下記書籍が参考になりました。

戦略的データサイエンス入門 ―ビジネスに活かすコンセプトとテクニック

戦略的データサイエンス入門 ―ビジネスに活かすコンセプトとテクニック (日本語) 単行本（ソフトカバー） – 2014/7/19 Foster Provost (著), Tom Fawcett (著), 竹田正和(監訳) (翻訳), 古畠敦 (翻訳), 瀬戸山雅人 (翻訳), & 7 その他

Amazon

楽天

Yahoo!ショッピング

評価はがちゃがちゃしましたが、モデルの学習自体は、結構いつも通りのやり方でいっています。

投票モデルで soft で学習させる場合って、決定木系のモデルは、あまり predict_proba に傾向的な要素が入らないため、実は使わない方がいいのかな？とか個人的に気になったりしているのですが、どうなんでしょう。