先日はKaggleデータセットにあるプロテニスのツアーの勝敗データで、強さのモデリングをしてみました。

その後、同じくKaggleデータセットの中で、別に公開されている男子プロテニスのツアーの勝敗データを見つけました。
確認したところ、上記で使ったデータセットよりも詳細なポイントなどが入っていましたので、これを色々弄っていた結果について、書いてみようかと思います。
データセット
今回使ったデータセットは下記になります。
- https://www.kaggle.com/ehallmar/a-large-tennis-dataset-for-atp-and-itf-betting
テーブルはいくつか格納されていますが、使ったテーブルは all_matches.csv だけで、ATPツアーの試合結果のデータについて、割りと最近の2018年の試合まで含まれています。
試合結果に関する各カラムの意味について、実際に行われたゲームの結果と照らし合わせながら調べました。
いくつか合っているか微妙ですが、恐らく、以下の内容が入っていそうでした。
num_sets # 全体セット数 sets_won # 獲得セット数 games_won # 獲得ゲーム数 games_against # 喪失ゲーム数 tiebrakes_won # 獲得タイブレーク数? tiebrakes_total # 全体タイブレーク数? serve_rating # ? aces # エース数 double_faults # ダブルフォルト数 first_serve_made # ファーストサービスが入った数=first_serve_points_attempted first_serve_attempted # ファーストサービスをおこなった数 first_serve_points_made # ファーストサービス成功時の獲得ポイント数 first_serve_points_attempted # ファーストサービス成功時の全体ポイント数=first_serve_made second_serve_points_made # セカンドサービス成功時の獲得ポイント数 second_serve_points_attempted # セカンドサービス成功時の全体ポイント数 break_points_saved # 被ブレイクポイントを守備した数 break_points_against # 全体の被ブレイクポイント数 service_game_won # ? return_rating # ? first_serve_return_points_made # 相手ファーストサービス成功時(リターン)の獲得ポイント数 first_serve_return_points_attempted # 相手ファーストサービス成功時(リターン)の全体ポイント数 second_serve_return_points_made # 相手セカンドサービス成功時(リターン)の獲得ポイント数 second_serve_return_points_attempted # 相手セカンドサービス成功時(リターン)の全体ポイント数 break_points_made # ブレイクポイントを獲得した数 break_points_attempted # 全体のブレイクポイント数 return_games_played # service_points_won # サービスポイントを獲得した数 service_points_attempted # 全体のサービスポイント数 return_points_won # リターンポイントを獲得した数=first_serve_return_points_made+second_serve_return_points_made return_points_attempted # 全体のリターンポイント数=first_serve_return_points_attempted+second_serve_return_points_attempted total_points_won # トータルポイント獲得数=service_points_won+return_points_won total_points # プレイされた合計ポイント数=service_points_attempted+return_points_attempted player_vistory # 勝敗 boolean retirement # 棄権したかどうか? boolean won_first_set # ファーストセットを勝ったかどうか? boolean doubles # ダブルスかどうか masters # トーナメントのATPポイント(例:2000=グランドスラム) round_num # 何回戦か
サーブ力とリターン力の分析
潜在変数の仮定
上記のように、各試合ごとに、ファースト・セカンドサービスから取得できたポイントだったり、逆に相手がファースト・セカンドサービスからリターンで取得できたポイントが入っています。
各選手には、サーブが得意な選手やリターンが得意な選手がいると思います。
そこで、今回は、各選手にサーブ力とリターン力の潜在変数があると仮定して、これを因子分析で推定し定量化をしてみました。
データの読み込みと加工
結構なサイズのファイルで、一気に読み込むことは不可能でした。
チャンクで一部ずつ取り出して不要な部分削りながら読み込んで、データフレームを作成します。
def preprocess(df):
df = df.dropna()
df = df[df['doubles'] == 'f']
df = df[df['year'] >= 2016]
df = df.drop([
'start_date', 'end_date', 'location', 'prize_money', 'currency', 'player_id', 'opponent_id',
'serve_rating', 'service_games_won', 'return_rating', 'return_games_played', 'duration', 'seed', 'nation'
], axis=1)
return df
reader = pd.read_csv('./data/all_matches.csv', chunksize=100)
df_matches = pd.concat((preprocess(r) for r in reader), ignore_index=True)
len(df_matches) # 36591
最近のデータで分析したいので、2016年以降のデータに限定し、シングルスのみを取得しています。
データには、ファースト・セカンドサービスが何回中何回成功したか、ポイントがいくつ取れたかなどが入っています。
各試合でどのくらいのポイントが実施されたのかが異なりますので、その試合中での成功率やポイント率に変換します。
df_tmp = df_matches[df_matches['masters'] == 2000]
# ファーストサービス成功率
df_tmp.loc[:, 'first_serve_rate'] = df_tmp['first_serve_made']/df_tmp['first_serve_attempted']
# ファーストサービス成功時のポイント率
df_tmp.loc[:, 'first_serve_point_rate'] = df_tmp['first_serve_points_made']/df_tmp['first_serve_points_attempted']
# セカンドサービス成功率
df_tmp.loc[:, 'second_serve_rate'] = 1-df_tmp['double_faults']/df_tmp['second_serve_points_attempted']
# セカンドサービス成功時のポイント率
df_tmp.loc[:, 'second_serve_point_rate'] = df_tmp['second_serve_points_made']/df_tmp['second_serve_points_attempted']
# 相手ファーストサービス成功時のポイント率
df_tmp.loc[:, 'first_serve_return_point_rate'] = df_tmp['first_serve_return_points_made']/df_tmp['first_serve_return_points_attempted']
# 相手セカンドサービス成功時のポイント率
df_tmp.loc[:, 'second_serve_return_point_rate'] = df_tmp['second_serve_return_points_made']/df_tmp['second_serve_return_points_attempted']
# 勝敗
df_tmp.loc[df_tmp['player_victory'] == 't', 'victory'] = 1
df_tmp.loc[df_tmp['player_victory'] == 'f', 'victory'] = 0
get_cols = [
'player_name', 'first_serve_rate', 'first_serve_point_rate','second_serve_rate', 'second_serve_point_rate',
'first_serve_return_point_rate', 'second_serve_return_point_rate', 'victory'
]
df_tmp = df_tmp[get_cols]
このままだと、チャレンジャーなどの試合にも出場しているプレイヤー全員で処理してしまうことになり、分析対象が多くなりすぎますので、今回は2016年以降に開催されたグランドスラムに出場したことがあり、かつ、10回以上の白星をあげているプレイヤーに絞りました。
df_tmp = df_tmp.groupby('player_name').agg(['mean','count'])
df_tmp = df_tmp[(df_tmp['victory']['count'] >= 10) & (df_tmp['victory']['mean'] > 0)]
levels = df_tmp.columns.levels
labels = df_tmp.columns.labels
df_tmp.columns = [levels[0][i]+'_'+levels[1][j] for i, j in zip(labels[0], labels[1])]
df_tmp = df_tmp[[c+'_mean' for c in get_cols[1:]]]
df_tmp.columns = get_cols[1:]
df_tmp_n = (df_tmp-df_tmp.mean())/df_tmp.std()
df_tmp_n = df_tmp_n.dropna()
len(df_tmp_n) # 81
分析と結果の解釈
まずは各カラムで相関をとってみて、上記であげた因子が仮定できそうか確認してみます。
plt.figure(figsize=(6,5))
sns.heatmap(df_tmp.corr(), annot=True, vmax=1, vmin=-1, fmt='.2f', cmap=cm)
plt.show()
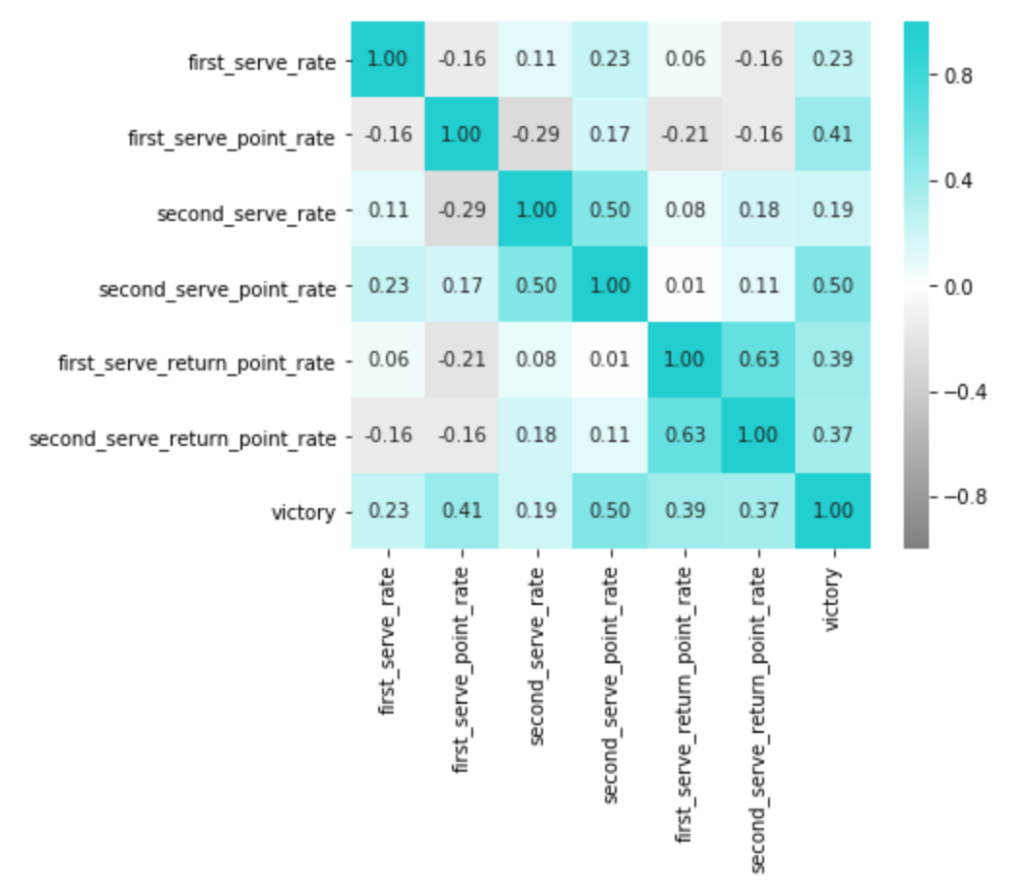
あれ...思ってたのとちょっと違う...。
これを見る限り、ファースト、セカンド両方とも、精度とポイント率はあまり相関しないようです。
言われてみれば当たり前ですが、精度とポイント率でみれば、勝敗に対して相関があるのはポイント率の方。
このクラスになると、もうサーブの精度なんてものは一定以上あって、よりその後のゲームメイクの方が重要になるようです。
また、これも意外だったのが、ファーストサービスからのポイント率とセカンドサービスからのポイント率が相関していないという点でした。
自分がサービスの時のゲーム展開が得意な選手の中でも、それがファーストの場合は得意であっても、セカンドの場合は得意とは限らない様子。
一方、リターンに関しては予想通りで、リターンが得意な選手は、相手がファーストでもセカンドでも、いずれも強い傾向があるようです。
この結果、最初の仮定では、サーブ力・リターン力の因子の数が2と仮定していましたが、ファーストサービス(のゲームメイク)力・セカンドサービス(のゲームメイク)力・リターン力の3つが潜在していると解釈できる結果になりそうな気がしてきました。
実際に分析にかけてみないと分からないので、因子数を2〜4で設定して、各結果について、因子負荷量と各選手の因子得点の様子を確認してみます。
因子の数を指定して、分析結果を返却する関数、分析結果から因子得点の散布図をプロットする関数を以下のように作成しました。
def fit(factor_num):
fa = decomposition.FactorAnalysis(n_components=factor_num).fit(x)
df_factor_loading = pd.DataFrame(columns=target_cols)
for i in range(factor_num):
df_factor_loading = df_factor_loading.append(pd.Series(fa.components_[i], index=target_cols, name='factor'+str(i)))
display(df_factor_loading)
return fa
def plot(factor_num, fa):
transformed = fa.fit_transform(x)
for i, j in itertools.combinations(np.arange(factor_num), 2):
plt.figure(figsize=(8,8))
plt.scatter(transformed[:, i], transformed[:, j], color=base_color)
for k, y_ in enumerate(y):
plt.annotate(y_, xy=(transformed[k, i], transformed[k, j]), size=8, alpha=0.5)
fai = fa.components_[i]
faj = fa.components_[j]
for k, c in enumerate(target_cols):
plt.arrow(0, 0, fai[k]*2, faj[k]*2, color='r', head_width=0.1, alpha=1)
plt.text(fai[k]*2.5, faj[k]*2.5, c, color='r', fontsize=12)
plt.axes().add_patch(plt.Circle((0, 0), radius=0.5*2, ec='r', fill=False))
plt.xlim([-3,3])
plt.ylim([-3,3])
plt.xlabel('factor'+str(i))
plt.ylabel('factor'+str(j))
plt.title('factor'+str(i)+' x '+'factor'+str(j))
plt.show()
return transformed
分析にかけるベクトルは以下です。
x = df_tmp_n[target_cols].values y = df_tmp_n.index
因子数2の場合
まずは因子数2の場合で、因子負荷量を確認してみます。
fa2 = fit(factor_num=2)

transformed2 = plot(factor_num=2, fa=fa2)
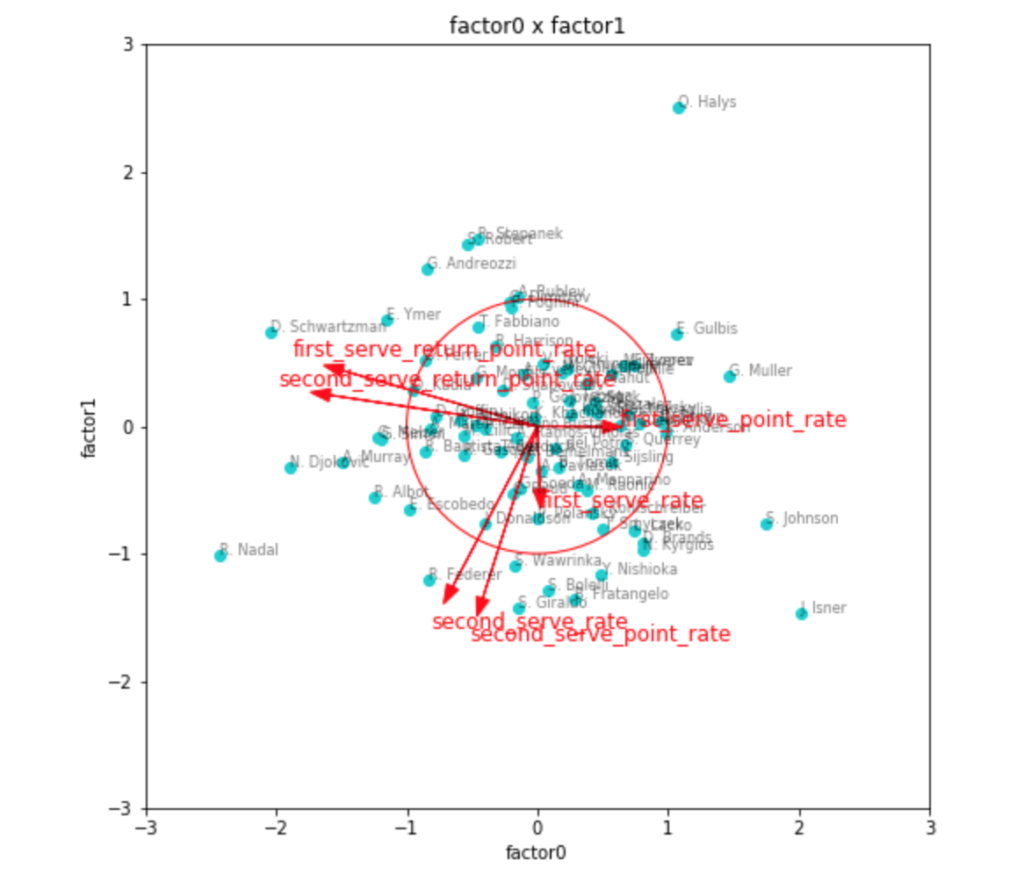
因子得点のプロットには、因子負荷量のベクトルと目安の0.5の円を同時に描いてみました。
やはり、これで見ると、リターン力に関しては1つの因子として取れそうですが、サーブに関する情報がうまくまとまらなさそうです。
因子数3の場合
次に因子数3の場合です。
fa3 = fit(factor_num=3)

transformed3 = plot(factor_num=3, fa=fa3)
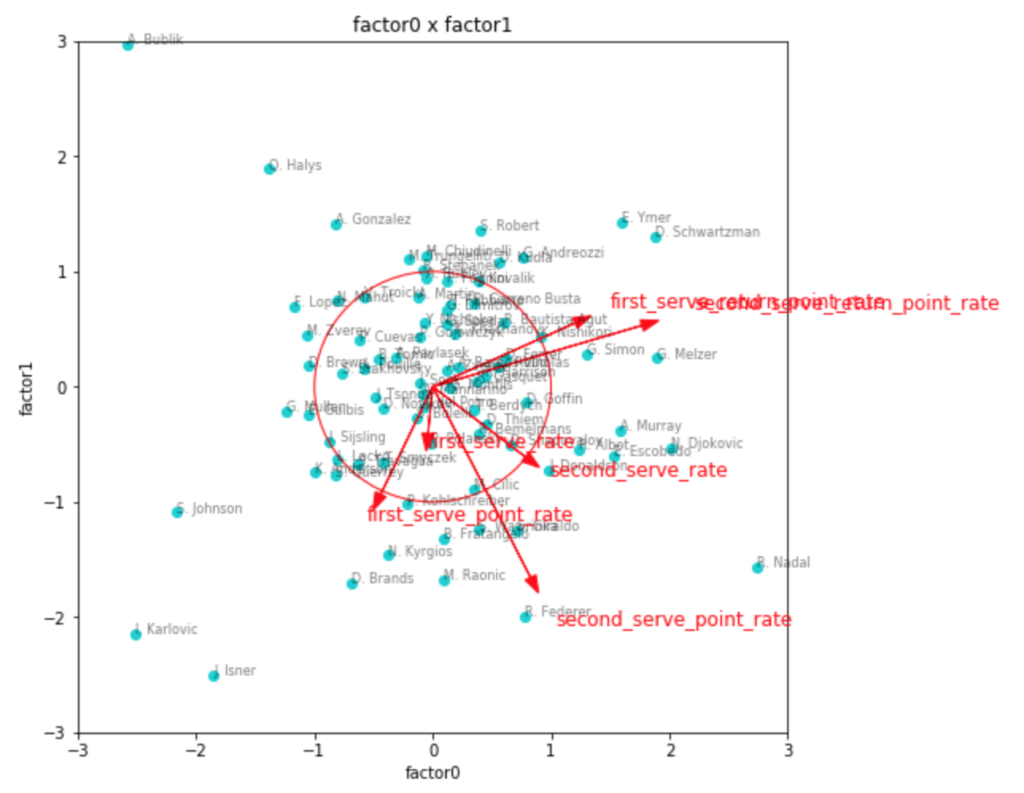
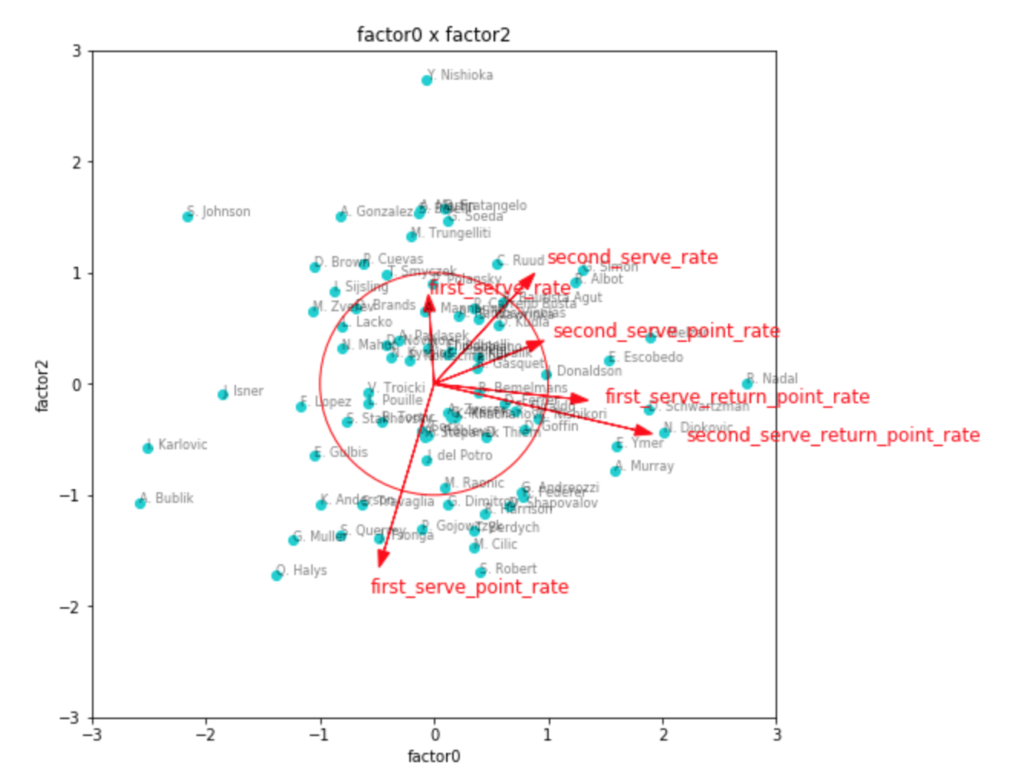
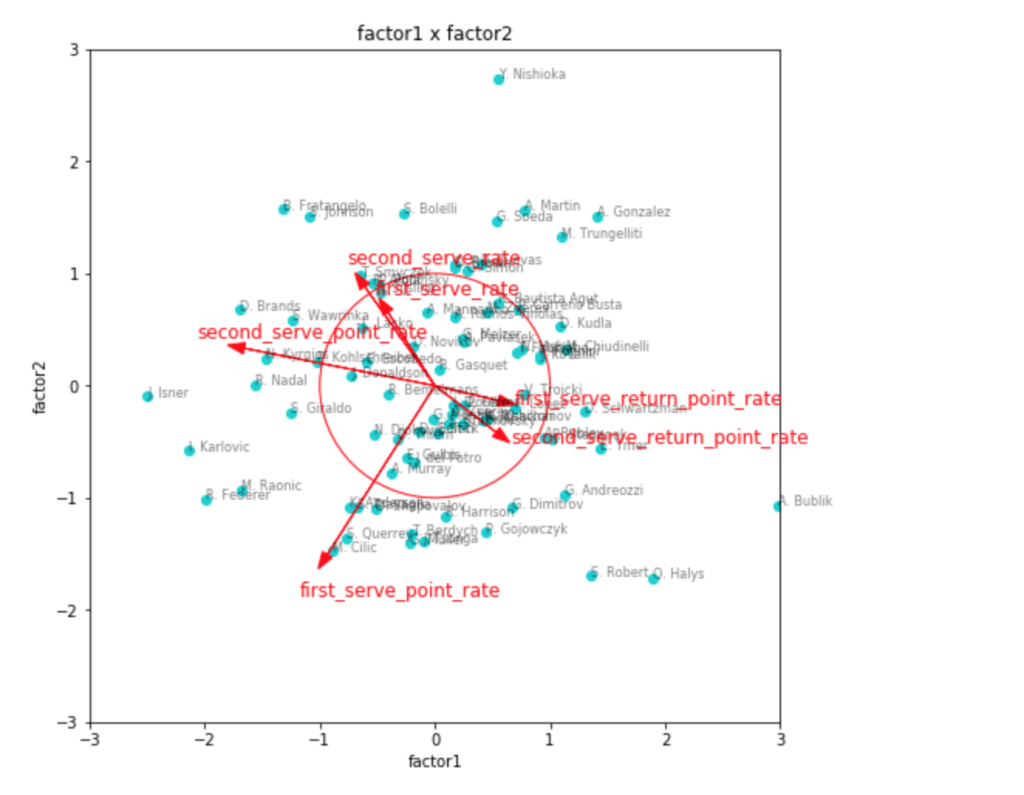
因子負荷量を見ても、やはりこれが一番しっくりきそう。
第1因子がリターン力、第2因子がセカンドサービスでのポイント力、第3因子がファーストサービスでのポイント力といったところでしょうか。
因子得点の3つ目のグラフなど見ると、見事に左下にビッグサーバー選手が集まっていて面白いです。
ファーストサービス方向にチリッチやクエリー、アンダーソンなどの選手がいて、かつセカンドサービス方向にも強いと位置しているのが、フェデラーやラオニッチ、カルロビッチといった選手で、サービスが武器と言われている選手の中でも、勝率としてより成功している選手は、両方の軸で強い位置に出てきているように見えます。
リターン力で見ると、ナダルやジョコビッチ、シュワルツマンなどが強いようですね。
ちょっと重なって見えづらいですが、錦織選手も強い位置にいます。
因子数4の場合
最後に因子数4の場合もやってみます。
fa4 = fit(factor_num=4)

うーん、なんだかよくわからなくなりました笑
因子負荷量の絶対値がどれもそこそこの大きさになってしまって、どの因子が何を表しているのか分からなくなってしまったので、これに関しては因子得点のプロットは省略します。
感想とまとめ
以上を見る限り、今回のデータからは、因子は、ファーストサービス(のゲームメイク)力・セカンドサービス(のゲームメイク)力・リターン力の3つから生成されると解釈した方が良さそうです。
勝率との相関を見てみると...
df_results = pd.DataFrame(
np.concatenate([np.array(y).reshape(len(y), 1), transformed3, df_tmp['victory'].values.reshape(len(y), 1)], axis=1),
columns = ['player_name', 'factor0', 'factor1', 'factor2', 'victory_rate']
)
df_results['factor0'] = df_results['factor0'].astype(np.float32)
df_results['factor1'] = -df_results['factor1'].astype(np.float32)
df_results['factor2'] = -df_results['factor2'].astype(np.float32)
df_results['victory_rate'] = df_results['victory_rate'].astype(np.float32)
plt.figure(figsize=(6,5))
sns.heatmap(df_results.corr(), annot=True, vmax=1, vmin=-1, fmt='.2f', cmap=cm)
plt.show()
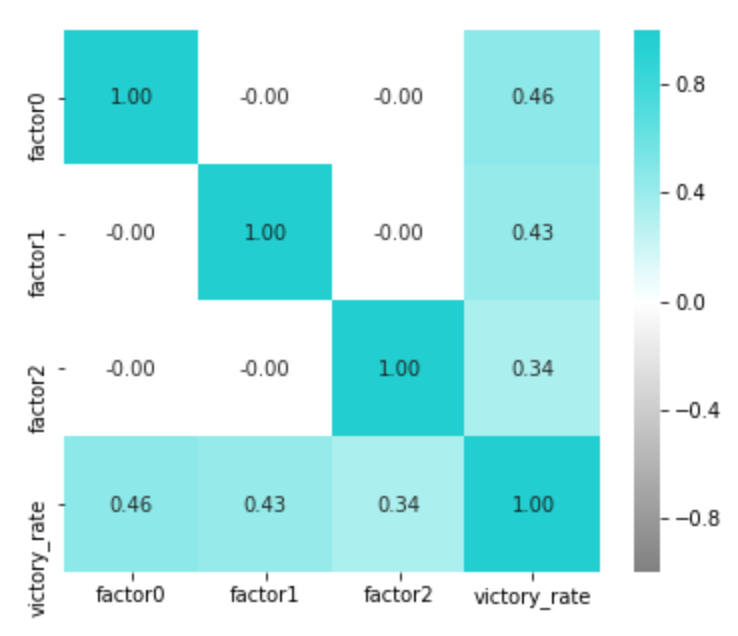
どれも大事。
ロジスティック回帰分析などにかけてみても面白そうでしたけど、今回はひとまずここまでで。
正直なところ、ある程度はうまくいったのかなと思うものの、やはり各因子の因子負荷量が、もう少し相関があるカラムとないカラムでキッパリと分かれてほしかったところもあります。
第2因子でみれば、セカンドサービスの強さを表していると共に、ファーストサービスのポイント率にもかなり相関していますので、第2因子だけでファーストおよびセカンドサービスの強さと表せそうな気がしないでもないんですよね。
最後に、これらの因子得点で見た錦織選手の順位について調べてみると、
print('K. Nishikori')
print('-'*50)
for i in [0, 1, 2]:
rank = np.where(df_results.sort_values(by='factor'+str(i), ascending=False)['player_name'].values == 'K. Nishikori')
rank = rank[0][0]+1
print('factor'+str(i), '\t', rank, '/', len(df_results))

となりました。
リターン力はかなりの上位に来ていて、その一方で、セカンドサーブからやられてしまう傾向があるみたいで、これは試合などを見ていても割と納得できる結果となりました。
今回の実装は下記にあげました。
コメント