以前、統計検定2級を受験しました。

今回は統計検定2級の受験対策に関して記そうと思います。
以前に準1級の対策についても記していますので、準1級の試験対策については、以下を参照してください。

参考書籍
(初級者向け)マンガでわかる統計学
私は元々理系出身のため、確率や統計の基本的な部分の勉強には、そこまで苦労はしませんでした。
しかし、最近では文系出身の方にも、統計検定取得の需要が高まってきている様子を感じています。
そこで、数式が苦手な初級者に関しては、少し古い書籍ですが、上記の書籍がとてもおすすめなので紹介します。
統計学はやはり数学なので、統計学のやさしい教科書であったとしても、やはり抽象的な表現が中心となってしまいます。
その辺りの統計学の数式のイメージを、世の中的にはどう解釈すれば良いのかの紐付けのきっかけになるような書籍だと思います。
(初級者向け)スバラシク実力がつくと評判の統計学キャンパス・ゼミ
こちらもどちらかといえば初級者向きの書籍です。
大学生の統計学の勉強の参考書となっていますので、初めて統計学を勉強する人に向いていると思います。
例えば、確率密度関数から、平均や分散を計算する時の計算の過程なども解説されているため、下記で紹介する統計検定2級対応の教科書で、数式が追えない場合はこちらを参照すると良いと思います。
また、上記書籍の演習版として、下記もおすすめです。
改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎
統計検定2級対応の公式教科書です。
上記2冊は、数学が苦手という初級者向けに紹介しましたが、そうでない人は、教科書はこの1冊で十分です。
説明は割りと初学者には厳し目ですので、初学者の人は、いきなりこれを読んで分からなかったとしても落ち込む必要はありません。
上記2冊などで入門してから読んだ方が良いです。
内容については、公式の教科書だけあって、統計検定2級までに出てくる範囲について、コンパクトにまとめられていると思います。
この書籍に記されている内容を理解できれば、十分合格できると思います。
また、これまでの過去問に一切出題されていない部分に関しては、理解が間に合ってなくても大丈夫だと思います。
例えば、仮説検定でいえば、![]() 検定や
検定や ![]() 検定は定番の問題としてよく出題されますが、相関係数の検定などは出題されること自体が少ないです。
検定は定番の問題としてよく出題されますが、相関係数の検定などは出題されること自体が少ないです。
まずは必ずといっても良いほど出題される範囲を優先的に理解していくと良いと思います。
後述に、覚えておくべき範囲(確率分布、仮説検定、区間推定)についてまとめましたので、参照して下さい。
ちなみに書籍は、改訂版の方が練習問題も記載されており、おすすめです。
また、中身の練習問題に関しては、公式の統計検定のホームページにて、「練習問題の解説(詳説)」が記載されていますので、こちらも併せて活用すると良いと思います。(2級教科書の項目)
- http://www.toukei-kentei.jp/info/books/#b1
日本統計学会公式認定 統計検定 2級 公式問題集
2級の過去問集です。
どのような資格試験においても、過去問の勉強は重要です。
また、直近の過去問は公式ページでもダウンロードができます。
統計検定 過去問: http://www.toukei-kentei.jp/past/
過去問を使った勉強としては、下記のようにサイクルを回して使うと良いと思います。
- 公式ダウンロードできる直近の過去問以外の過去問を全て解答する
- わからなかった問題に(時間制限も意識して、すぐに解答が思い浮かばなかったものも含め)チェックを入れておく
- チェックしたところを、解答や教科書を参考にしながら勉強をする(ここで教科書の練習問題なども解いてみる)
- 再度、わからなかったところのみ解答する
- 上記をチェックがなくなるまで繰り返す
- 最後に、全ての過去問と、直近の過去問も含めて解答する
- わからなかったところを復習して、再度解答する
以上のように過去問をサイクルを回していって、順番に分からないところを潰していきます。
何回も解いていると、出題の傾向や解答のコツなどもだんだんとわかってきて、自然と合格ラインに乗ってくると思います。
上記の過去問集の前に出版されている、実施年が古い方の過去問題集もあるので、下記に添付しておきます。
上記の過去問の実施年とも被っているので、勉強時間に余裕があったり、上記の問題だけでは不安であれば、活用すると良いと思います。
44の例題で学ぶ統計的検定と推定の解き方
特に区間推定や仮説検定の範囲で理解度が怪しくて、もっと問題を解いてみたいという場合には、この書籍がおすすめです。
文字通り、区間推定・仮説検定の問題集+解説の書籍です。
上記の公式教科書で説明した通り、2級でよく出題される範囲を中心に活用すると良いかと思います。
よく出題される確率分布
統計検定2級では、色々な確率分布について出題されます。
2級対応の教科書にも色々な確率分布について記されていますが、全てを把握しておく必要はないと思います。
例えば、離散分布の中でも、二項分布やポアソン分布はよく出題されやすい傾向がありますが、負の二項分布や超幾何分布はあまり出題されません。
個人的に、最低限これだけ勉強しておけば良いだろうと思う確率分布を、以下にリスト化しました。
確率(密度)関数から平均と分散を自分で計算できるまで理解できれば良いですが、余裕がなければ覚えてしまっても良いと思います。
| 確率分布 | 説明 | 離散/連続 | 確率(密度)関数 | 平均 | 分散 |
|---|---|---|---|---|---|
| ベルヌーイ分布 |
成功する確率が |
離散 | |||
| 二項分布 |
成功する確率が |
離散 | |||
| 幾何分布 |
成功する確率が |
離散 | |||
| ポアソン |
単位時間あたりに平均 |
離散 | |||
| 一様分布 |
変数の幅を固定した場合にどこでも確率が一定となる分布 | 離散・連続 | 指数分布 |
単位時間当たりの生起回数が期待値 |
連続 |
| 正規分布 |
期待値 |
連続 | |||
確率分布の範囲に関しては、実際に問題文から、従う分布は何で、確率関数が何かまで分かっていないと手がつけられないような問題であったり、または後述する区間推定や仮説検定の範囲の中で、知っている前提として出題されることが多いように思いますので、少なくとも上記の確率分布においては、しっかり理解をしておくと良いと思います。
よく出題される区間推定・仮説検定
統計学を初めて学ぶ人はここで躓く人が多いと聞きます。
基本的にこの辺りの手法のモチベーションは、少ないサンプルデータから、どうにかして母集団の性質を知りたいということになります。
区間推定も仮説検定もやることは同じであり、
- 前提や仮説の上で、(検定)統計量が従う確率分布の確率分布表と、問題で与えられた有意確率(1%や5%など)から、統計量の値がとりうる範囲を求める
- 前提や仮説の上で、(検定)統計量の値を求める
- 上記の2つを比較する
この時の範囲が、区間推定の場合は信頼区間、仮説検定の場合は棄却域と呼ばれている違いがあるというだけです。
区間推定では、99%や95%の確率で母集団の真の統計量はこの範囲(信頼区間)に入っているだろうとみなすことを意味し、仮説検定では、帰無仮説を棄却したい(仮説を否定して母集団の性質を知りたい)という目的があり、帰無仮説が正しい時に99%や95%の確率でとりうる確率変数の値の範囲から外れてほしい(1%や5%という滅多に起こらない値をとっているから仮説が間違っているとみなす)という違いを表しています。
また、ここでいう確率分布は、![]() 分布やカイ二乗分布、
分布やカイ二乗分布、![]() 分布などを表します。
分布などを表します。
これらの分布もいきなり出てきた上に抽象的で躓きやすいですが、これらは、上記で紹介したような、世の中の事柄を表すための確率分布ではなく、こういった区間推定や仮説検定などの時に使うための確率分布です。
例えば、![]() 分布が生まれた経緯には、
分布が生まれた経緯には、
 検定で平均の検定をしようとしたけど、母分散が未知であった
検定で平均の検定をしようとしたけど、母分散が未知であった- 母分散の推定値を代用して検定統計量を作成した
- それは当然、標準正規分布に従わない(かなり似ているが厳密には違った)ので、どういう分布なのか、確率密度関数を明らかにした
- それが
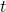 分布と呼ばれるようになった
分布と呼ばれるようになった
といった流れがあったりします。
だから、こういった検定などに利用される分布に関しては、付表が記載されています。
こういった世の中の事柄を表すためのものではない確率分布というものは他にもたくさんあります。
例えば、話が逸れますが、ベータ分布やディリクレ分布などは確率の確率を表しており、ベイズ統計モデルなどに用いられます。
長々と記してしまいましたが、仮説検定・区間推定について、2級合格には、下記の手法を中心的に覚えておけば問題ないかと思います。
この辺りの範囲についても、確率分布の時の範囲と同じで、教科書には乗っているけど、あまり出題されないような、例えば、無相関検定などは無視しておいても構わないと思います。(業務では割と使ったりしますが...)
| 対象とする統計量 | 区間推定 | 仮説検定 | 利用する確率分布(付表) | 備考 | |
|---|---|---|---|---|---|
| 信頼区間 | 帰無仮説 |
検定統計量 | |||
| 母分散が既知の場合の母平均 | 標準正規分布 | ||||
| 母分散が未知の場合の母平均 | 自由度 |
||||
| 母分散 | 自由度 |
||||
| 母比率 | 標準正規分布 | ||||
| 母分散が既知の場合の対応のない母平均の差 | 標準正規分布 | ||||
| 母分散が未知の場合の対応のない母平均の差(等分散) | 自由度 |
||||
| 母分散の比 | 自由度 |
||||
| 母比率の差 | 標準正規分布 | ||||
2標本間の母平均の差では、色々なパターンにより微妙に変わるので、問題文を読んだときに、どれを使うべきかが適切に判断できるように注意して下さい。
対応がある場合は、対応しているサンプルデータごとの差分がまた正規分布に従うため、![]() の場合は1標本の時の標準正規分布による母平均の手法、
の場合は1標本の時の標準正規分布による母平均の手法、 ![]() の場合は1標本の時の
の場合は1標本の時の ![]() 分布による母平均の手法を使うことになります。
分布による母平均の手法を使うことになります。
また、母分散が未知の場合の検定に関しては、![]() や
や ![]() が大きくなれば、
が大きくなれば、![]() 分布は正規分布に近づくため、例えば、
分布は正規分布に近づくため、例えば、![]() や
や ![]() の場合は、母分散が未知であっても、母分散が既知の場合の分散に不偏標本分散を代入して、同様の検定を行うことができます。
の場合は、母分散が未知であっても、母分散が既知の場合の分散に不偏標本分散を代入して、同様の検定を行うことができます。
母分散が未知の場合かつ非等分散である場合は、ウェルチの ![]() 検定と呼ばれるものが使えますが、これはあまり出題されない傾向にあるようですので、ひとまず合格に向けては覚えなくても大丈夫だと思います。
検定と呼ばれるものが使えますが、これはあまり出題されない傾向にあるようですので、ひとまず合格に向けては覚えなくても大丈夫だと思います。
また、上記らのように一つの統計量のみに注目しているものではありませんが、以下の仮説検定もよく出題されますので、勉強しておくと良いと思います。
- 未知母数がない場合の適合度の検定
- 未知母数がある場合の適合度の検定
- 独立性の検定
いずれの検定も、用いる確率分布は ![]() 分布です。
分布です。
適合度の検定は、与えられたサンプルデータが、どのような確率分布に従う(適合する)かを確かめる検定です。
その確率分布には、母数(パラメータ)が含まれることがあります。(ポアソン分布に従うか確かめる場合は ![]() など)
など)
未知母数が云々という話は、この母数が未知なのか既知なのかによって、![]() 分布の自由度が変わるということです。
分布の自由度が変わるということです。
また、この辺りに対して必要な理解度についてですが、2級合格を目標とするならば、ひとまずはやり方を覚えておくだけ十分かと思います。
仮説検定や区間推定に関しては、踏み込んだ話そこまで求められていないように思います。
踏み込んだ話というのは、いわゆる、検定統計量がどのような理屈で導かれているのかといったところだったりです。
そこまでよりも、まずは、問題の題意からどの手法を使えば良いのかを選択でき、得られた結果の解釈を正しくできれば問題ありません。
- 題意から検定統計量を見極める
- それが棄却域に含まれている(信頼区間に含まれていない)ならば、母集団は帰無仮説の性質を持っていないだろうとみなす
- 逆に含まれていない(信頼区間に含まれている)ならば、与えられたサンプルデータでは、母集団が帰無仮説の性質を持つことが十分にありえる(帰無仮説の性質を持っていないとは言い切れない)とみなす
といった感じに作業的に覚えておくと良いでしょう。
また、解答はマーク式ですので、検定統計量の値を求めるだけで選択肢が半分に減ったりなどしますので、計算はしっかりとできるようにしておくと良いと思います。
以上までを危なげなく出来るようになってきてから、どういった仕組みで検定統計量が導かれたのかなどを勉強してみても良いかと思います。
この辺りの話は、やり方に則って行うだけだと気持ち悪いと思うかもしれませんが、モチベーションを理解した上で、どういったカラクリでそのモチベーションを解決しようとしているのかが分かると、とても腑に落ちると思います。
電卓について
統計検定では電卓を持ち込むことができますが、いわゆる関数電卓のような高性能な電卓を持ち込むことはできません。
以下、公式の統計検定の2級のページ引用です。
使用可の電卓
四則演算(+-×÷)や百分率(%)、平方根(√)の計算ができる一般電卓又は事務用電卓
使用不可の電卓
上記の電卓を超える計算機能を持つ関数電卓やプログラム電卓、電卓機能を持つ携帯端末
電卓は、確率の計算や検定統計量などの計算に用いることになります。
検定統計量の計算によっては、少数がどこまでも続くような数が出てくることもあり、さらにそれを使って別の計算までさせていくとなっていくと、少数が浅いところで切っていると多少誤差が出てきてしまいます。
解答はマーク式ですので、それでも一番近いものを選べば大抵間違いないのですが、選択肢にかなり近い数にならないと不安で仕方がないという人は、表示できる桁数の多い電卓を使うと良いでしょう。(といっても、解答の方が割りと大きくズレていることもあったりしますが)
また、ボタンが大きくて押しやすく、滑り止めがついている、液晶が傾けられるなど、下記のような電卓を持っていっても大丈夫なので、おすすめです。
私は1回、ボタンがゴム式の安物の電卓を使って問題集を解いた時がありましたが、ボタンの反応が悪いことがあり、結果、押し損ないによる計算ミスややり直しなどが多々発生していましたので、その辺りも注意しておくと、本番が安心かと思います。










コメント